I. Vue d'ensemble▲
Dans cette section, nous présentons un aperçu de Scilab. Le premier chapitre présente le projet open source associé à la création de ce document. Ensuite, nous présentons les aspects logiciels, licences et scientifiques de Scilab. Dans le troisième chapitre, nous décrivons les méthodes pour télécharger et installer Scilab sur les systèmes d'exploitation Windows, GNU/Linux et Mac. Dans les autres chapitres, nous décrivons différentes sources d'informations utiles pour obtenir de l'aide depuis Scilab ou de la part d'autres utilisateurs. Nous décrivons les pages d'aide intégrées et nous analysons les listes de diffusion et le wiki qui sont disponibles en ligne. Enfin, nous prenons un moment pour regarder les démonstrations qui sont fournies avec Scilab.
I-A. Introduction▲
Ce document est un projet open source. Les sources LATEX sont disponibles sur la forge Scilab : http://forge.scilab.org/index.php/p/docintrotoscilab/.
Les sources LATEX sont fournies selon les termes de la licence « Creative Commons Attribution - Partage dans les Mêmes Conditions 3.0 non transposé » : http://creativecommons.org/licenses/by-sa/3.0/deed.fr.
Les scripts Scilab sont disponibles sur la forge, à l'intérieur du projet, dans le sous-répertoire « scripts ». Les scripts sont disponibles sous la licence CeCILL : http://www.cecill.info/licences/Licence_CeCILL_V2-fr.txt.
I-B. Aperçu de Scilab▲
Scilab est un langage de programmation associé à une riche collection d'algorithmes numériques couvrant de nombreux aspects des problèmes de calcul scientifique.
Du point de vue logiciel, Scilab est un langage interprété. Ceci accélère généralement le processus de développement, parce que l'utilisateur accède directement à un langage de haut niveau, avec un riche ensemble de fonctionnalités offertes par la bibliothèque. Le langage Scilab est destiné à être étendu afin que des types de données « utilisateurs » puissent être définis par d'éventuelles opérations de surcharge. Les utilisateurs de Scilab peuvent développer leurs propres modules afin de résoudre leurs problèmes particuliers. Le langage Scilab peut compiler et lier dynamiquement d'autres langages tels que Fortran et C : de cette façon, des bibliothèques externes peuvent être utilisées comme si elles faisaient partie des fonctionnalités intégrées de Scilab. Scilab s'interface également avec LabVIEW, une plate-forme et un l'environnement de développement pour le langage de programmation visuel de National Instruments.
Du point de vue de la licence, Scilab est un logiciel gratuit et open source, sous licence Cecill [2]. Le logiciel est distribué avec le code source, de telle sorte que l'utilisateur dispose d'un accès aux aspects les plus internes de Scilab. La plupart du temps, l'utilisateur télécharge et installe une version binaire de Scilab, car le consortium Scilab fournit les versions exécutables pour Windows, Linux et Mac OS. L'aide en ligne est disponible dans de nombreuses langues.
Du point de vue scientifique, Scilab est livré avec de nombreuses fonctionnalités. Au tout début de Scilab, les fonctionnalités se sont concentrées sur l'algèbre linéaire. Mais, rapidement, leur nombre s'est élargi pour couvrir de nombreux domaines de l'informatique scientifique. Voici une courte liste de ses capacités :
- algèbre linéaire, matrices creuses ;
- polynômes et fractions rationnelles ;
- interpolation, approximation ;
- optimisation linéaire, quadratique et non linéaire ;
- solveur d'équations différentielles ordinaires et solveur d'équations différentielles algébriques ;
- commande classique et robuste, optimisation par inégalité matricielle linéaire ;
- optimisation différentiable et non différentiable ;
- traitement du signal ;
- statistiques.
Scilab offre de nombreuses fonctionnalités graphiques, y compris un ensemble de fonctions de traçage, qui créent des tracés 2D et 3D ainsi que des interfaces utilisateur. L'environnement Xcos fournit un modeleur et un simulateur hybride de systèmes dynamiques.
I-C. Comment obtenir et installer Scilab ?▲
Quelle que soit votre plate-forme (Windows, Linux ou Mac), les binaires Scilab peuvent être téléchargés directement à partir de la page d'accueil Scilab : http://www.scilab.org ou à partir de l'espace de téléchargement : http://www.scilab.org/download.
Les binaires sont fournis pour les plates-formes 32 et 64 bits afin de correspondre à la machine d'installation cible.
Scilab peut également être téléchargé sous forme de source, de sorte que vous pouvez compiler Scilab par vous-même et produire votre propre binaire. Compiler Scilab et générer un binaire est particulièrement intéressant lorsque l'on veut comprendre ou déboguer une fonction existante, ou lorsqu'on souhaite ajouter une nouvelle fonctionnalité. Pour compiler Scilab, certains fichiers binaires prérequis sont nécessaires, et sont également prévus dans l'espace de téléchargement. En outre, un compilateur Fortran et un compilateur C sont nécessaires. La compilation de Scilab ne sera pas détaillée dans ce document.
I-C-1. Installation de Scilab sous Windows▲
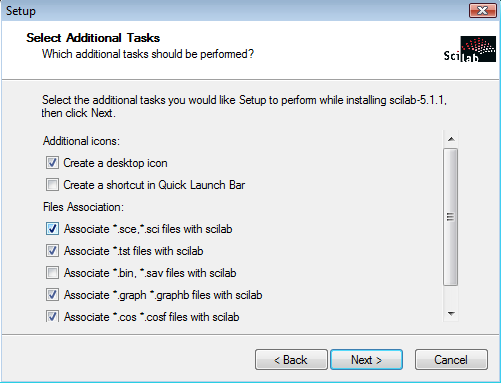
Scilab est distribué sous forme binaire pour Windows et un programme d'installation est fourni pour que l'installation soit vraiment facile. La console Scilab est présentée dans la Figure 1.
Sous Windows, si votre machine est basée sur un processeur Intel, la bibliothèque Intel Math Kernel Library (MKL) [6] permet à Scilab d'effectuer des calculs numériques plus rapides.
I-C-2. Installation de Scilab sous Linux▲
Sous Linux, les versions binaires sont disponibles sur le site de Scilab sous la forme d'un fichier « .tar.gz ». Il n'y a pas besoin de programme d'installation avec Scilab sous Linux : il suffit de décompresser le fichier dans un répertoire cible. Une fois cela fait, le fichier binaire se trouve dans le <path>/scilab5.xx/bin/scilab. Lorsque ce script est exécuté, la console apparaît immédiatement et ressemble exactement à celle sur Windows.
Notez que Scilab est également distribué avec le système de paquets disponible avec les distributions Linux basées sur Debian (par exemple Ubuntu). Cette méthode d'installation est extrêmement simple et efficace. Néanmoins, il a un petit inconvénient : la version de Scilab empaquetée pour votre distribution Linux peut ne pas être à jour. C'est parce qu'il y a un peu de retard (de quelques semaines à plusieurs mois) entre la disponibilité d'une mise à jour du logiciel Scilab sous Linux et sa publication dans les distributions Linux.
Pour l'instant, sous Linux, Scilab est fourni avec une bibliothèque d'algèbre linéaire binaire qui garantit la portabilité. Sous Linux, Scilab n'est pas fourni avec une version binaire d'ATLAS [1], de sorte que l'algèbre linéaire est un peu plus lente pour cette plate-forme, par rapport à Windows.
I-C-3. Installation de Scilab sous Mac OS▲
Sous Mac OS, les versions binaires sont disponibles sur le site de Scilab sous la forme d'un fichier « .dmg ». Ce binaire fonctionne pour les versions Mac OS à partir de la version 10.5. Il utilise le programme d'installation de Mac OS, ce qui fournit un processus d'installation classique. Scilab n'est pas disponible sur les systèmes Power PC.
Pour des raisons techniques, la version 5.3 de Scilab pour Mac OS X est livrée avec une interface Tcl/Tk désactivée. En conséquence, il y a quelques légères limitations sur l'utilisation de Scilab sur cette plate-forme. Par exemple, l'interface Scilab/Tcl (TclSci) et l'éditeur graphique ne fonctionnent pas. Ces fonctionnalités seront réécrites en langage Java dans les futures versions de Scilab et ces limitations disparaîtront.
Pourtant, l'utilisation de Scilab sur un système Mac OS est facile, et utilise les raccourcis qui sont familiers pour les utilisateurs de cette plate-forme. Par exemple, la console et l'éditeur utilisent la touche Cmd (touche pomme) qui se trouve sur les claviers Mac. En outre, il n'existe aucun clic droit de la souris sur cette plate-forme. À la place, Scilab est sensible à la combinaison de touches clavier « Control+clic ».
Pour l'instant, sur Mac OS, Scilab est fourni avec une bibliothèque d'algèbre linéaire qui est optimisée et qui garantit la portabilité. Sous Mac OS, Scilab n'est pas fourni avec une version binaire d'ATLAS [1], de sorte que l'algèbre linéaire est un peu plus lente pour cette plate-forme.
I-D. Comment obtenir de l'aide ?▲
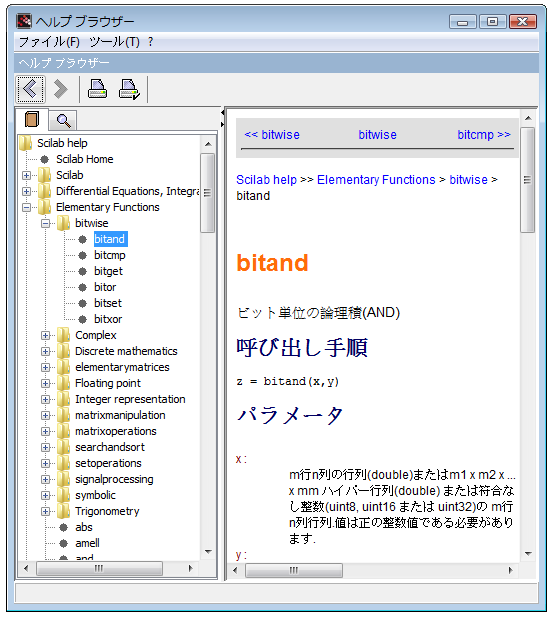
La façon la plus simple d'obtenir l'aide en ligne intégrée à Scilab est d'utiliser la fonction help. La figure 2 présente la fenêtre d'aide de Scilab.
Pour utiliser cette fonction, il suffit de taper « help » dans la console et d'appuyer sur la touche Entrée, comme dans l'exemple suivant :
helpSupposons que vous vouliez de l'aide sur la fonction optim. Vous pouvez essayer de consulter l'aide intégrée, trouver la section « Optimization », puis cliquer sur l'élément « optim » pour afficher son aide.
Une autre possibilité est d'utiliser la fonction help, suivie du nom de la fonction, pour laquelle une aide est nécessaire, comme ceci :
help optimScilab ouvre automatiquement l'entrée associée dans l'aide. Nous pouvons également utiliser l'aide fournie sur le site Web de Scilab : http://www.scilab.org/product/man.
Cette page contient toujours l'aide de la version mise à jour du logiciel Scilab. En utilisant la fonction « Recherche » du navigateur, il est possible, la plupart du temps, de trouver rapidement la page d'aide dont on a besoin. Avec cette méthode, on peut voir les pages d'aide de plusieurs commandes Scilab en même temps (par exemple les commandes derivative et optim, afin de pouvoir fournir la fonction de coût appropriée pour l'optimisation avec optim en calculant les dérivées avec derivative).
Une liste de livres payants et gratuits, de tutoriels en ligne et d'articles est présentée sur la page d'accueil Scilab : http://www.scilab.org/publications.
I-E. Listes de diffusion, forum, wiki et rapports de bogue▲
Il existe plusieurs listes de diffusions disponible à cette adresse : http://www.scilab.org/development/ml. La liste de diffusion users@lists.scilab.org est conçue pour toutes les questions d'utilisation de Scilab. La liste de diffusion dev@lists.scilab.org se concentre sur le développement de Scilab, que ce soit le développement du noyau Scilab ou de modules complexes qui interagissent fortement avec le noyau Scilab. Ces listes de diffusion sont archivées aux adresses : http://dir.gmane.org/gmane.comp.mathematics.scilab.user et : http://dir.gmane.org/gmane.comp.mathematics.scilab.devel. Par conséquent, avant de poser une question, les utilisateurs devraient envisager de regarder dans l'archive si la même question ou le sujet a déjà obtenu une réponse.
Un forum Scilab en français est disponible sur Developpez.com à cette adresse : https://www.developpez.net/forums/f1715/environnements-developpement/autres-edi/scilab/.
Une question peut être liée à un point technique très spécifique, de sorte qu'elle exige une réponse qui n'est pas assez générale pour être publique. L'adresse est prévue à cet effet. Les développeurs de l'équipe Scilab fournissent des réponses précises via ce canal de communication.
Le wiki Scilab est un outil public pour la lecture et la publication d'informations générales sur Scilab : http://wiki.scilab.org. Il est utilisé à la fois par les utilisateurs de Scilab et par les développeurs pour publier des informations sur Scilab. Du point de vue du développeur, il contient un guide étape par étape des instructions pour compiler Scilab à partir des sources, les dépendances de différentes versions de Scilab, les instructions d'utilisation du référentiel de code source Scilab, etc.
Le « Scilab's Bug Tracker » (http://bugzilla.scilab.org) permet de soumettre un rapport à chaque fois qu'un nouveau bogue est trouvé. Il peut arriver que celui-ci a déjà été découvert par quelqu'un d'autre. C'est pourquoi il est conseillé de rechercher dans la base de données de bogues pour des problèmes similaires existants avant de signaler un nouveau bogue. Si le bogue n'est pas signalé à ce jour, c'est une très bonne chose de le signaler, avec un script de test. Ce script de test doit rester aussi simple que possible pour reproduire le problème et identifier la source du problème.
Une façon efficace de se tenir à jour des informations est d'utiliser des flux RSS. Le flux RSS associé avec le site Scilab est http://www.scilab.org/en/rss_en.xml. Ce canal fournit régulièrement des communiqués de presse et les annonces générales.
I-F. Comment obtenir de l'aide à partir des démonstrations Scilab et des macros ?▲
Le consortium Scilab possède une collection de scripts de démonstration, qui sont disponibles à partir de la console, dans le menu « ? > Scilab Demonstrations ». La figure 3 présente la fenêtre de démonstration.
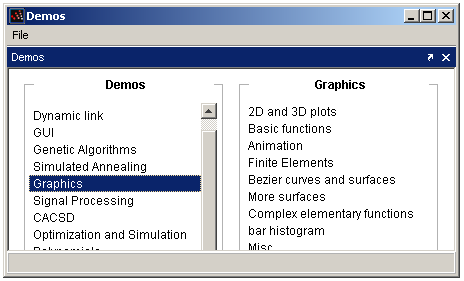
Certaines démonstrations sont graphiques, tandis que d'autres sont interactives, ce qui signifie que l'utilisateur doit taper sur la touche Entrée pour passer à la prochaine étape de la démonstration.
Les scripts de démonstrations associés sont situés dans le répertoire Scilab, à l'intérieur de chaque module. Par exemple, la démonstration associée au module d'optimisation est située dans le fichier : <path>\scilab-5.3.1\modules\optimization\demos\datafit\datafit.dem.sce. Bien sûr, le chemin exact du fichier dépend de votre installation et de votre système d'exploitation.
L'analyse du contenu de ces fichiers de démonstration est souvent une solution efficace pour résoudre les problèmes courants et pour comprendre les caractéristiques particulières.
Une autre méthode pour trouver de l'aide est d'analyser le code source de Scilab lui-même (Scilab est en effet open source !). Par exemple, la fonction derivative se trouve dans : <path>\scilab-5.3.1\modules\optimization\macros\derivative.sci.
La plupart du temps, les macros Scilab sont très bien écrites, en prenant soin de toutes les combinaisons possibles d'arguments d'entrée et de sortie et de nombreuses valeurs possibles des arguments d'entrée. Souvent, des problèmes numériques difficiles sont résolus dans ces scripts. Vous pouvez donc vous en inspirer pour l'élaboration de vos propres scripts.
I-G. Exercices▲
Exercice I.1 - Installation de Scilab
Installez la version actuelle du logiciel Scilab sur votre système (au moment où ce document est écrit, c'est Scilab v5.3.3). Il est instructif d'installer une version plus ancienne de Scilab, afin de comparer le comportement actuel par rapport à l'ancien. Installez par exemple Scilab 4.1.2 et voyez les différences.
Exercice I.2 - L'aide en ligne : derivative
La fonction derivative calcule la dérivée d'une fonction numérique. Le but de cet exercice est de trouver la page d'aide correspondante, par divers moyens. Dans l'aide intégrée, trouvez l'entrée correspondante de la fonction derivative. Trouvez l'entrée correspondante dans l'aide en ligne. Utilisez la console pour trouver l'aide.
Exercice I.3 - Poser une question sur le forum
Vous avez probablement déjà une ou plusieurs questions. Postez votre question sur le forum Scilabou sur la mailing list des utilisateurs.
II. Mise en route▲
Dans cette section, nous faisons nos premiers pas avec Scilab et nous présentons certaines tâches simples que nous pouvons effectuer avec l'interpréteur.
Il y a plusieurs façons d'utiliser Scilab et les paragraphes qui suivent présentent trois méthodes :
- à l'aide de la console en mode interactif ;
- en utilisant la fonction exec avec un fichier ;
- en utilisant le traitement par lots.
Nous présentons également la gestion des fenêtres graphiques avec le système d'ancrage. Enfin, nous présentons deux caractéristiques principales de Scilab : la localisation, qui fournit des messages et les pages d'aide dans la langue de l'utilisateur et le système ATOMS, un système d'empaquetage pour les modules externes.
II-A. La console▲
La première façon consiste à utiliser Scilab de façon interactive, en tapant des commandes dans la console, en analysant les résultats et en poursuivant ce processus jusqu'à ce que le résultat final soit calculé. Ce document est conçu de telle sorte que les exemples de Scilab qui y sont fournis peuvent être copiés dans la console. L'objectif est que le lecteur puisse expérimenter le comportement de Scilab par lui-même. C'est en effet un bon moyen de comprendre le comportement du programme et, la plupart du temps, il s'agit d'un moyen rapide et en douceur d'effectuer le calcul désiré.
Dans l'exemple suivant, la fonction disp est utilisée dans le mode interactif pour imprimer la chaîne « Hello World! ».
-->s="Hello World!"
s =
Hello World!
-->disp(s)
Hello World!Dans l'exemple précédent, nous n'avons pas à saisir les caractères « --> » qui représentent l'invite, gérée par Scilab. Nous tapons simplement la déclaration s="Hello World!" avec notre clavier et puis nous appuyons sur la touche Entrée. Scilab répond s = et Hello World!. Puis on tape disp(s) et Scilab répond Hello World!.
Quand nous saisissons une commande, nous pouvons utiliser le clavier, comme avec un éditeur ordinaire. Nous pouvons utiliser les touches fléchées <←> et <→> pour déplacer le curseur sur la ligne et utiliser les touches <Backspace> et <Suppr> afin de corriger les erreurs dans le texte.
Afin d'obtenir l'accès aux commandes précédemment exécutées, nous utilisons la touche fléchée <↑>. Cela nous permet de parcourir les commandes précédentes en utilisant les touches fléchées <↑> et <↓>.
La touche <Tab> fournit une fonctionnalité d'autocomplétion très pratique. Dans l'exemple suivant, on tape l'instruction disp dans la console :
-->dispEnsuite, on peut taper sur la touche <Tab>, ce qui fait apparaître une liste dans la console, telle que présentée dans la Figure 4. Scilab affiche une liste, où les éléments correspondent à toutes les fonctions qui commencent par les lettres « disp ». On peut alors utiliser les touches fléchées <↑> et <↓> pour sélectionner la fonction que nous voulons.
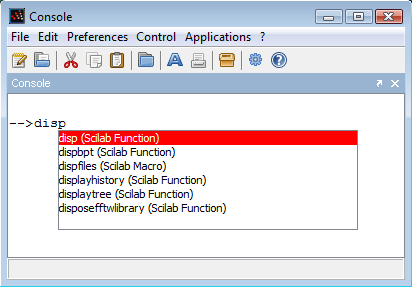
L'autocomplétion fonctionne avec les fonctions, les variables, les fichiers et les identifiants graphiques et rend le développement de scripts plus facile et plus rapide.
II-B. L'éditeur▲
La version 5.3 de Scilab fournit un éditeur pour éditer facilement les scripts. La figure 5 présente l'éditeur lors de l'édition de l'exemple précédent « Hello World! ».
L'éditeur est accessible depuis le menu de la console, sous le menu « Applications > Editor », ou depuis la console, comme présenté à l'exemple suivant :
--> editor()Cet éditeur gère plusieurs fichiers en même temps, comme dans la Figure 5, où cinq fichiers sont édités en même temps.
Il y a beaucoup de caractéristiques qui méritent d'être mentionnées à propos de cet éditeur. Les caractéristiques les plus couramment utilisées sont dans le menu « Execute ».
- « Load into Scilab » exécute les instructions dans le fichier courant, comme si on faisait un copier-coller. Ceci implique que les déclarations qui ne se terminent pas par un point-virgule « ; » produiront une sortie dans la console ;
- « Evaluate Selection » exécute les instructions qui sont actuellement sélectionnées ;
- « Execute File Into Scilab » exécute le fichier, comme si nous avions utilisé la fonction exec. Les résultats qui sont produits dans la console ne sont que ceux qui sont associés à des fonctions d'affichage, comme disp.
Nous pouvons aussi sélectionner quelques lignes dans le script, faire un clic droit (ou « Cmd + clic » sous Mac), et obtenir le menu contextuel qui est présenté à la Figure 6.
Le menu « Edit » contient une fonctionnalité très intéressante. Il s'agit de la fonction « Edit > Correct Indentation », qui indente automatiquement la sélection en cours. Cette fonction est très pratique, car elle formate les algorithmes, de sorte que les blocs if, for et autres soient faciles à analyser.
L'éditeur fournit un accès rapide à l'aide en ligne. En effet, supposons que nous choisissions la déclaration disp, tel que présenté dans la figure 7. Quand nous faisons un clic droit dans l'éditeur, on obtient le menu contextuel, où l'entrée « Help on selection » ouvre la page d'aide associée à la fonction disp.
II-C. Ancrage▲
Les graphismes de la version Scilab 5 ont été mis à jour de sorte que de nombreux composants sont désormais basés sur Java. Cela a un certain nombre d'avantages, notamment la possibilité de gérer l'ancrage des fenêtres.
Le système d'ancrage utilise FlexDock [12], un projet open source fournissant un framework d'ancrage Swing. Supposons que nous ayons à la fois la console et l'éditeur ouverts dans notre environnement, tel que présenté dans la figure 8. Il pourrait être gênant de gérer les deux fenêtres, car l'une pourrait cacher l'autre, de sorte que nous devrions constamment les déplacer afin de voir réellement ce qui se passe.
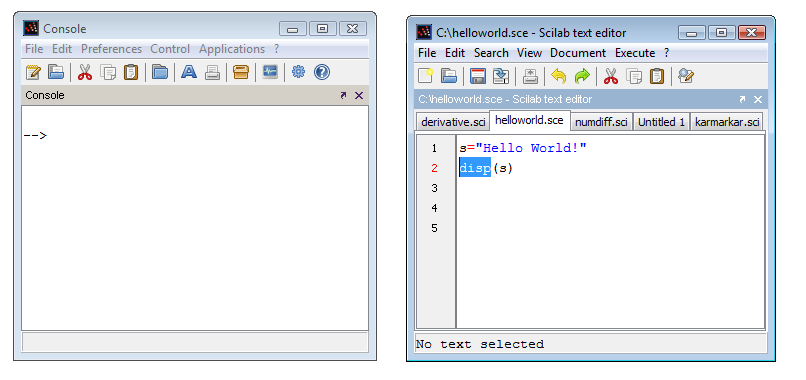
Le système FlexDock nous permet de faire glisser et de déposer l'éditeur dans la console, de sorte que nous ayons enfin une seule fenêtre, avec plusieurs sous-fenêtres. Toutes les fenêtres Scilab peuvent être ancrées, y compris la console, l'éditeur, le navigateur de variable, l'historique des commandes, l'aide et les fenêtres de tracé. Dans la Figure 9, nous présentons une situation où nous avons ancré quatre fenêtres dans la fenêtre de la console.

Afin d'ancrer une fenêtre à une autre fenêtre, il faut faire glisser la fenêtre source dans la fenêtre cible. Pour ce faire, nous faisons un clic gauche sur la barre de titre de la fenêtre d'accueil, comme indiqué dans la figure 8. Avant de relâcher le clic, nous allons passer la souris sur la fenêtre cible et nous notons que la fenêtre est affichée entourée de pointillés. Cette fenêtre « transparente » indique l'emplacement de la future fenêtre. Nous pouvons choisir cet emplacement, qui peut être sur le haut, le bas, la gauche ou la droite de la fenêtre cible. Une fois que nous avons choisi l'emplacement cible, nous relâchons le clic, ce qui déplace finalement la fenêtre source dans la fenêtre cible, comme dans la figure 9.
Nous pouvons également libérer la fenêtre source sur la fenêtre de cible, ce qui crée des onglets, comme dans la figure 10.
II-D. Le navigateur de variable et l'historique des commandes▲
Scilab fournit un navigateur de variable (« variable browser », qui affiche la liste des variables utilisées actuellement dans l'environnement. La figure 11 présente l'état de ce navigateur au cours d'une session.
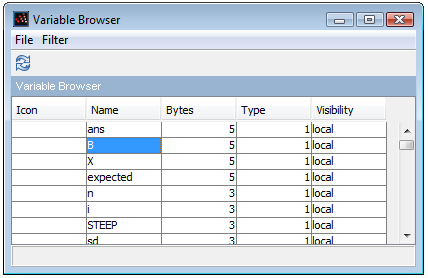
Nous pouvons accéder à ce navigateur via le menu « Applications > Variable Browser », mais la fonction browsevar() a le même effet.
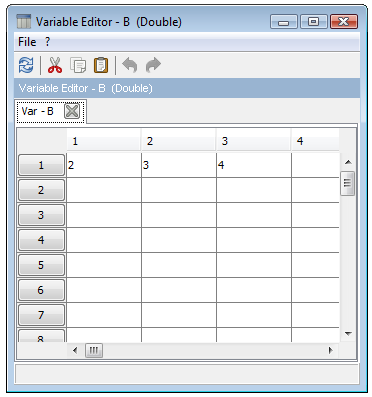
On peut double-cliquer sur une variable, ce qui ouvre l'éditeur de variables, tel que présenté dans la Figure 12.
On peut alors changer de façon interactive la valeur d'une variable en changeant son contenu dans une cellule. D'autre part, si l'on change le contenu d'une variable à l'intérieur de la console, il faut actualiser le contenu de la boîte de dialogue en appuyant sur le bouton d'actualisation dans la barre d'outils de l'éditeur de variables.
La boîte de dialogue « Command History » permet de naviguer à travers les commandes que nous avons précédemment exécutées. Cette boîte de dialogue est disponible dans le menu « Applications > Command History » et est présentée dans la Figure 13.
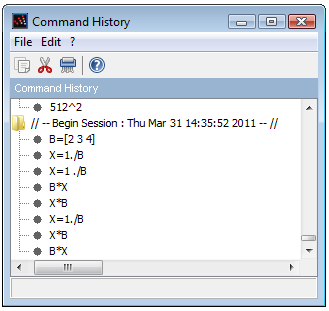
On peut sélectionner n'importe quelle commande dans la liste et double-cliquer dessus pour l'exécuter dans la console. Le clic droit ouvre un menu contextuel qui nous permet d'évaluer la commande ou l'éditer dans l'éditeur.
II-E. Utiliser exec▲
Lorsque plusieurs commandes doivent être exécutées, il peut être plus commode d'écrire ces déclarations dans un fichier avec l'éditeur de Scilab. Pour exécuter les commandes situées dans un tel fichier, la fonction exec peut être utilisée, suivie par le nom du script. Ce fichier a généralement l'extension .sce ou .sci, en fonction de son contenu :
- les fichiers ayant l'extension .sci contiennent des fonctions Scilab et les exécuter charge les fonctions dans Scilab (mais ne les exécute pas) ;
- les fichiers ayant l'extension .sce contiennent à la fois des fonctions Scilab et des instructions exécutables.
Exécuter un fichier .sce a généralement pour effet de calculer plusieurs variables et d'afficher les résultats dans la console, de créer des tracés 2D, de lire ou d'écrire dans un fichier, etc.
Supposons que le contenu du fichier myscript.sce soit le suivant :
disp("Hello World !")Dans la console Scilab, nous pouvons utiliser la fonction exec pour exécuter le contenu de ce script :
-->exec("myscript.sce")
-->disp("Hello World !")
Hello World !Dans les situations pratiques, telles que le débogage d'un algorithme complexe, le mode interactif est utilisé la plupart du temps avec une séquence d'appels aux fonctions exec et disp.
II-F. Exécution par lot▲
Une autre façon d'utiliser Scilab est depuis la ligne de commande. Plusieurs options de ligne de commande sont disponibles et sont présentées dans la liste suivante :
- -e instruction : exécute l'instruction Scilab indiquée dans « instruction » ;
- -f fichier : exécute le script Scilab donné dans le fichier ;
- -l langue : configure la langue de l'utilisateur, par exemple, "fr" pour le français et "en" pour l'anglais (la valeur par défaut est "fr") ;
- -mem N : définit la taille de la pile initiale ;
- -ns : si cette option est présente, le fichier de démarrage scilab.start n'est pas exécuté ;
- -nb : si cette option est présente, alors la bannière de bienvenue Scilab ne s'affiche pas ;
- -nouserstartup : n'exécute pas les fichiers de démarrage de l'utilisateur SCIHOME/.scilab ou SCIHOME/scilab.ini ;
- -nw : débute Scilab en ligne de commande avec des fonctionnalités avancées (par exemple graphiques) ;
- -nwni : débute Scilab en ligne de commande sans fonctionnalités avancées ;
- -version : affiche la version du produit et sort.
Quel que soit le système d'exploitation, les binaires sont situés dans le répertoire scilab-5.3.1/bin. Les options de ligne de commande doivent être jointes à l'application pour la plate-forme spécifiquement, comme décrit ci-dessous :
- sous Windows, deux exécutables binaires sont fournis. Le premier exécutable est WScilex.exe, comme d'habitude, la console interactive, graphique et usuelle. Cet exécutable correspond à l'icône qui se trouve sur le bureau après l'installation de Scilab. Le second exécutable est Scilex.exe, la console non graphique. Avec l'exécutable Scilex.exe, la console Java n'est pas chargée et le terminal Windows est utilisé directement. Le programme Scilex.exe est sensible aux options -nw et -nwni ;
- sous Linux, le script Scilab fournit des options qui configurent son comportement. Par défaut, le mode graphique est lancé. Le script Scilab est sensible aux options -nw et -nwni. Il y a deux exécutables supplémentaires sur Linux : scilab-cli et scilab-adv-cli. L'exécutable scilab-adv-cli est équivalent à l'option -nw, tandis que scilab-cli est équivalent à l'option -nwni [7].
- sous Mac OS, le comportement est similaire à la plate-forme Linux.
L'option -nw désactive l'affichage de la console. L'option -nwni lance le mode non graphique : dans ce mode, la console ne s'affiche pas et les fonctions de traçage sont désactivées (les utiliser génère une erreur).
Dans l'exemple suivant sous Windows, on lance le programme Scilex.exe avec l'option -nwni. Ensuite, nous exécutons la fonction plot afin de vérifier que cette fonction n'est pas disponible dans le mode non graphique.
D:\Programs\scilab-5.3.1\bin>Scilex.exe -nwni
___________________________________________
scilab -5.3.1
Consortium Scilab (DIGITEO)
Copyright (c) 1989-2011 (INRIA)
Copyright (c) 1989-2007 (ENPC)
___________________________________________
Startup execution:
loading initial environment
-->plot()
!--error 4
Undefined variable: plotL'option de ligne de commande la plus utile est l'option -f, qui exécute les commandes depuis un fichier donné, une méthode généralement appelée traitement par lots. Supposons que le contenu du fichier « myscript2.sce » soit le suivant :
disp("Hello World !")
quit()où la fonction quit est utilisée pour sortir de Scilab.
Le comportement par défaut de Scilab est d'attendre une entrée utilisateur : c'est pourquoi la commande quit est utilisée, de sorte que la session se termine. Pour exécuter la démonstration sous Windows, nous avons créé le répertoire « C:\scripts » et écrit les instructions dans le fichier « C:\Scripts\myscript2.sce ». L'exemple suivant, exécuté à partir d'un terminal Windows, montre comment utiliser l'option -f pour exécuter le script précédent. Notez que nous avons utilisé le chemin absolu de l'exécutable Scilex.exe.
C:\scripts>D:\Programs\scilab-5.3.1\bin\Scilex.exe -f myscript2.sce
___________________________________________
scilab -5.3.1
Consortium Scilab ( DIGITEO )
Copyright (c) 1989 -2011 ( INRIA )
Copyright (c) 1989 -2007 ( ENPC )
___________________________________________
Startup execution :
loading initial environment
Hello World !
C:\scripts>Toute ligne qui commence par deux caractères barre oblique « // » est considérée par Scilab comme un commentaire et est ignorée. Pour vérifier que Scilab reste par défaut en mode interactif, nous mettons en commentaire la déclaration quit avec la syntaxe « // », comme dans le script suivant :
disp("Hello World !")
// quit()Si nous tapons la commande scilex -f myscript2.sce dans le terminal, Scilab attendra désormais une entrée utilisateur, comme prévu. Pour quitter, nous tapons interactivement la déclaration quit() dans le terminal.
II-G. Localisation▲
Par défaut, Scilab fournit ses messages et ses pages d'aide dans la langue anglaise. Mais il peut aussi les fournir en français, en chinois, en portugais et en plusieurs autres langues. Dans cette section, nous passons en revue ces éléments et nous voyons leurs effets dans Scilab.
Les fonctions de localisation de Scilab changent deux fonctionnalités différentes dans Scilab :
- les messages de l'application de Scilab (menus, messages d'erreur…) ;
- les pages d'aide.
La liste suivante présente les langues prises en charge par Scilab 5.3.2 pour l'application elle-même. Pour certaines de ces langues, les pages d'aide de Scilab sont (partiellement) traduites, comme indiqué entre parenthèses.
- ca_ES : catalan - Espagne ;
- de_DE : allemand - Allemagne ;
- en_US : anglais - États-Unis ;
- es_ES : espagnol de Castille - Espagne ;
- en_FR : français-France (avec pages d'aide) ;
- it_IT : italien - Italie ;
- ja_JP : japonais - Japon (avec pages d'aide) ;
- pl_PL : polonais - Pologne ;
- pt_BR : portugais - Brésil (avec pages d'aide) ;
- ru_RU : russe - Fédération de Russie ;
- uk_UA : ukrainien - Ukraine ;
- zh_CN : chinois simplifié ;
- zh_TW : chinois traditionnel.
Scilab fournit plusieurs fonctions qui gèrent la localisation. Ces fonctions sont présentées dans la liste suivante :
- getdefaultlanguage : renvoie la langue utilisée par défaut par Scilab ;
- getlanguage : renvoie la langue actuellement utilisée par Scilab ;
- setdefaultlanguage : définit et enregistre la valeur interne LANGUAGE ;
- setlanguage : définit la valeur interne LANGUAGE ;
- dgettext : traduit le texte dans la localisation et le domaine spécifique en cours ;
- gettext : traduit le texte dans la localisation et le domaine en cours.
Sous Windows, on peut utiliser la fonction setdefaultlanguage, qui prend une chaîne représentant la langue souhaitée comme argument d'entrée. Puis nous redémarrons Scilab pour que les menus de la console soient convertis. Dans l'exemple suivant, nous utilisons la fonction setdefaultlanguage afin de configurer la langue portugaise.
setdefaultlanguage("pt_BR")Lorsque nous redémarrons Scilab, les messages d'erreur sont fournis en portugais :
-->1+"foo"
!--error 144
Operação indefinida para os dados operandos.
Verifique ou defina a função %s_a_c para overloading.La figure 17 présente la page d'aide de la fonction bitand en japonais.
Sous GNU/Linux, Scilab utilise la langue du système d'exploitation, de sorte que la plupart des utilisateurs devraient obtenir Scilab dans leur propre langue sans configurer Scilab. Par exemple, dans Ubuntu, l'installation et la configuration de langues peuvent être faites dans le menu « System > Administration > Language Support ».
Sous GNU/Linux ou Mac OS X, une autre façon de démarrer Scilab dans une autre langue est de définir la variable d'environnement LANG. Par exemple, la commande suivante dans le terminal Linux lance Scilab en japonais :
# Starts Scilab in Japanese
LANG = ja_JP scilabPourtant, il pourrait y avoir des différences entre la langue utilisée par GNU/Linux, et la langue utilisée par Scilab. Ces différences peuvent provenir d'une mauvaise définition de la langue, où Scilab ne peut pas trouver le langage qui correspond à celui attendu. Quand nous lançons Scilab depuis un terminal Linux, le message suivant peut s'afficher :
$ Warning : Localization issue .
Does not support the locale '' ( null ) C.
( process :1516): Gtk - WARNING **:
Locale not supported by C library .
Using the fallback 'C' locale .Une cause fréquente de cette erreur est les différentes façons de définir une langue. Notez, par exemple, qu'il y a une différence entre la langue « fr » (le français) et la langue « fr_FR » (le français en France). Dans ce cas, nous devons configurer la langue « fr_FR », qui est la langue détectée par Scilab. Une autre raison, en particulier sur la distribution Debian GNU/Linux, c'est que la locale pourrait ne pas avoir été compilé. Dans ce cas, nous pouvons utiliser la commande dpkg-reconfigure locales dans le terminal Linux.
Plus d'informations sur la localisation de Scilab sont fournies à [8].
II-H. ATOMS, le système de paquetage de Scilab▲
Dans cette section, nous présentons ATOMS, qui est un ensemble d'outils conçus pour installer des boîtes à outils prédéfinies.
Scilab est conçu pour être étendu par les utilisateurs, qui peuvent créer de nouvelles fonctions et les utiliser comme si elles étaient distribuées avec Scilab. Ces extensions sont appelées « boîtes à outils » ou « modules externes ». La création d'un nouveau module, avec ses pages d'aide associées et les tests unitaires, est relativement simple et c'est une partie du succès de Scilab.
Cependant, la plupart des modules ne peuvent pas être utilisés directement sous forme de source : le module doit être compilé pour que les fichiers binaires puissent être chargés dans Scilab. Cette étape de compilation n'est pas simple et peut-être même impossible pour les utilisateurs qui veulent utiliser un module basé sur un code source C ou Fortran et qui n'ont pas de compilateur. C'est l'un des problèmes qu'a résolus ATOMS : les modules sont fournis sous forme binaire, ce qui permet à l'utilisateur d'installer un module sans phase de compilation et sans problème de compatibilité Scilab.
Une caractéristique supplémentaire pour l'utilisateur est que la plupart des modules sont disponibles sur toutes les plates-formes : les développeurs bénéficient de la ferme de compilation du Consortium Scilab et les utilisateurs bénéficient d'un module qui est, la plupart du temps, assuré d'être multiplate-forme.
ATOMS est le système de conditionnement de modules externes de Scilab. Avec cet outil, les modules Scilab existants (c'est-à-dire précompilés), peuvent être téléchargés, installés et chargés. Les dépendances sont gérées, de sorte que si un module A dépend d'un module B, l'installation du module A installe automatiquement le module B. Ceci est similaire au système de paquetage disponible dans la plupart des distributions GNU/Linux/BSD. Les modules ATOMS sont disponibles sur tous les systèmes d'exploitation sur lesquels Scilab est disponible, c'est-à-dire sous Microsoft Windows, GNU/Linux et Mac OS X. Par exemple, lorsqu'un module ATOMS est installé sur Scilab s'exécutant sur un système d'exploitation MS Windows, le module préconstruit correspond à la version de MS Windows du module et est installé automatiquement. Le portail web pour ATOMS est le suivant : http://atoms.scilab.org.
Ce portail présente la liste complète des modules ATOMS et laisse les développeurs de modules mettre en ligne leurs nouveaux modules. La liste suivante présente les dix modules ATOMS les plus téléchargés :
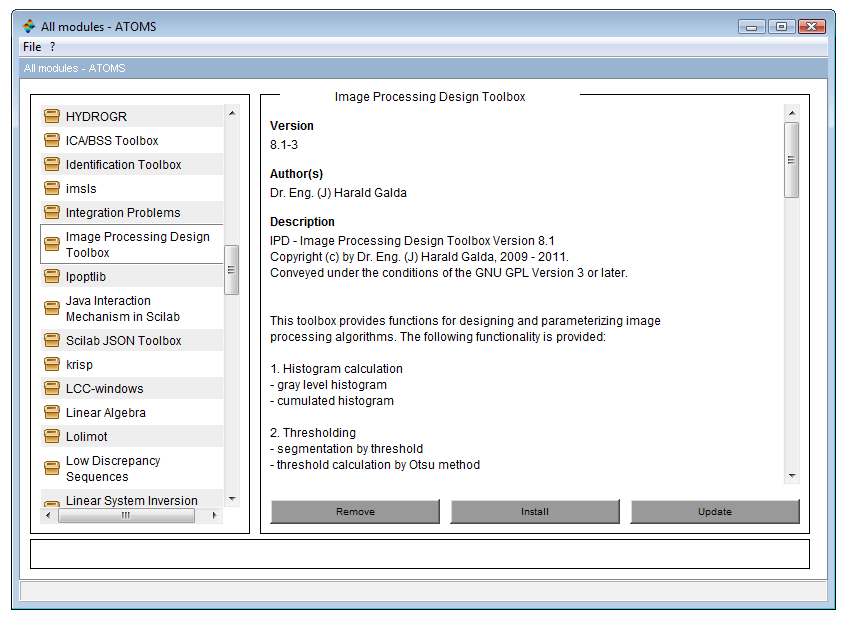
- Image Processing Design Toolbox (« IPD ») : fonctions pour la détection d'objets ;
- Scilab Image and Video Processing toolbox (« SIVP ») : traitement d'image et vidéo ;
- Plotting library (« plotlib ») : bibliothèque « Matlab-like » de tracé pour Scilab ;
- Scilab2C (« scilab2c ») : traduire du code Scilab en code C ;
- Apifun (« apifun ») : vérifier les arguments d'entrée dans les macros ;
- Module Lycée (« module_lycee ») : Scilab pour les lycées ;
- Guimaker (« guimaker ») : créer des interfaces graphiques avec un minimum de programmation ;
- Make Matrix (« makematrix ») : une collection de matrices de test ;
- GUI Builder (« guibuilder ») : un constructeur d'interface homme-machine (IHM) ;
- Scilab_XLL (« Scilab_XLL ») : ajout Scilab Xll pour Excel.
Ceci est juste une liste arbitraire de modules : plus de cent modules sont actuellement disponibles sur ATOMS.
Il y a deux façons d'installer un module ATOMS. La première méthode consiste à utiliser la fonction atomsGui, qui ouvre une interface utilisateur graphique qui permet à l'utilisateur de naviguer à travers tous les modules ATOMS disponibles. Cet outil est également disponible à partir du menu « Applications > Module manager - ATOMS » de la console Scilab. Dans l'interface graphique, nous pouvons lire la description du module et cliquer simplement sur le bouton « Install ». La Figure 19 présente l'interface graphique ATOMS.
La seconde manière est d'utiliser la fonction atomsInstall, qui prend le nom d'un module comme argument d'entrée. Par exemple, pour installer le module « makematrix », l'instruction suivante doit être exécutée :
atomsInstall("makematrix")Puis Scilab doit être redémarré et le module « makematrix » (et ses dépendances le cas échéant) est automatiquement chargé.
Plus de détails sur ATOMS sont disponibles à [9].
II-I. Exercices▲
Exercice II.1 - La console
Tapez la commande suivante dans la console :
atomsMaintenant, tapez sur la touche de tabulation. Qu'est-ce qui se passe ? Maintenant, tapez la lettre « I », puis tapez à nouveau sur la tabulation. Qu'est-ce qui se passe ?
Exercice II.2 - Utiliser exec
Lorsque nous développons un script Scilab, nous utilisons souvent la fonction exec en combinaison avec la fonction ls, qui affiche la liste des fichiers et répertoires dans le répertoire courant. Nous pouvons également utiliser la commande pwd, qui affiche le répertoire courant. La variable SCI contient le nom du répertoire de l'installation actuelle de Scilab. Nous l'utilisons très souvent pour exécuter les scripts qui sont fournis dans Scilab. Tapez les instructions suivantes dans la console et voyez ce qui se passe.
pwd
SCI
ls(SCI+"/modules")
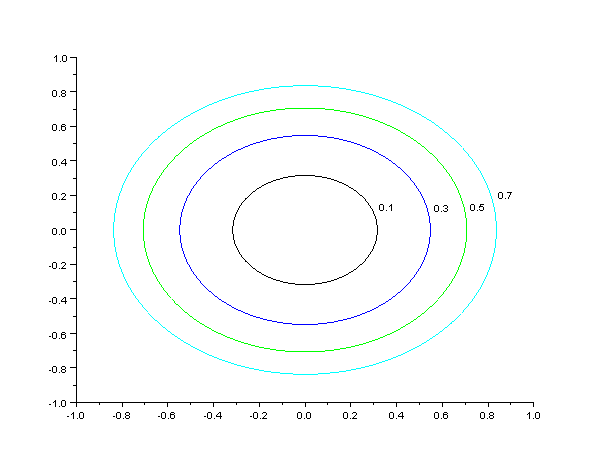
ls(SCI+"/modules/graphics/demos")
ls(SCI+"/modules/graphics/demos/2d_3d_plots")
dname = SCI+"/modules/graphics/demos/2d_3d_plots";
filename = fullfile(dname ,"contourf.dem.sce");
exec(filename)
exec(filename);III. Les éléments de base du langage▲
Scilab est un langage interprété, ce qui signifie que nous pouvons manipuler les variables de façon très dynamique. Dans cette section, nous présentons les caractéristiques de base du langage, c'est-à-dire, nous montrons comment créer une variable réelle, et quelles fonctions mathématiques élémentaires peuvent être appliquées à une variable réelle. Si Scilab ne proposait que ces caractéristiques, il ne serait qu'une supercalculatrice de bureau. Heureusement, il y a beaucoup plus, et c'est l'objet des sections restantes, où nous montrerons comment gérer les autres types de variables, c'est-à-dire les booléens, les nombres complexes, les entiers et les chaînes.
Cela peut sembler étrange au premier abord, mais il vaut mieux le dire dès le début : dans Scilab, tout est une matrice. Pour être plus précis, nous devrions écrire : toutes les variables réelles, complexes, booléennes, entières, chaîne et polynomiales sont des matrices. Les listes et les autres structures de données complexes (comme tlists et mlists) ne sont pas des matrices (mais peuvent contenir des matrices). Ces structures de données complexes ne seront pas présentées dans ce document.
C'est pourquoi nous pourrions commencer par présenter les matrices. Pourtant, nous avons choisi de présenter les types de données de base d'abord, car les matrices Scilab sont en fait une organisation particulière de ces blocs de construction de base.
Dans Scilab, nous pouvons gérer des nombres réels et complexes. Cela conduit toujours à une certaine confusion si le contexte n'est pas suffisamment clair. Dans ce qui suit, lorsque nous écrivons « variable réelle », nous allons nous référer à une variable dont le contenu n'est pas complexe. Les variables complexes seront abordées dans le chapitre III-G comme un cas particulier des variables réelles. Dans la plupart des cas, les variables réelles et les variables complexes se comportent d'une manière très similaire, même si quelques précautions supplémentaires doivent être prises lorsque des données complexes sont à traiter. Comme cela encombrerait la présentation, nous simplifions la plupart des discussions en ne considérant que les variables réelles, en ne prenant un soin supplémentaire avec des variables complexes que lorsque c'est nécessaire.
III-A. Création de variables réelles▲
Dans cette section, nous créons des variables réelles et effectuons des opérations simples avec elles.
Scilab est un langage interprété, ce qui implique qu'il n'y a pas besoin de déclarer une variable avant de l'utiliser. Les variables sont créées au moment où elles ont été fixées.
Dans l'exemple suivant, nous allons créer et définir la variable réelle x à 1 et effectuer une multiplication sur cette variable. Dans Scilab, l'opérateur « = » signifie que nous voulons définir la variable à gauche avec la valeur associée à droite (ce n'est pas l'opérateur de comparaison, dont la syntaxe est associée à l'opérateur « == »).
-->x=1
x =
1.
-->x = x * 2
x =
2.La valeur de la variable est affichée à chaque fois qu'une instruction est exécutée. Ce comportement peut être supprimé si la ligne se termine par un caractère point-virgule « ; », comme dans l'exemple suivant :
-->y=1;
-->y=y*2;Tous les opérateurs algébriques communs présentés dans la liste suivante sont disponibles dans Scilab :
- + : addition ;
- - : soustraction ;
- * : multiplication ;
- / : division à droite, i.e. x/y = xy-1 ;
- \ : division à gauche, i.e. x\y = x-1y ;
- ^ : puissance, i.e. xy ;
- ** : puissance (comme ^) ;
- ' : transposée conjuguée.
Notons que l'opérateur de puissance est représenté par le caractère « ^ » de telle sorte que le calcul de X2 dans Scilab est réalisé par l'expression « x^2 » ou de manière équivalente par l'expression « x**2 ». L'opérateur apostrophe « ' » sera présenté plus en détail dans le chapitre III-G, qui présente les nombres complexes. Il sera examiné à nouveau dans le chapitre IV-L, qui traite de la transposée conjuguée d'une matrice.
III-B. Les noms de variables▲
Les noms de variables peuvent être aussi longs que l'utilisateur le veut, mais seuls les 24 premiers caractères sont pris en compte dans Scilab. Par souci de cohérence, il convient de ne considérer que les noms de variables qui ne sont pas faits de plus de 24 caractères. Toutes les lettres ASCII de « a » à « z » et de « A » à « Z » et les chiffres de « 0 » à « 9 » sont autorisés, avec les caractères supplémentaires « % », « _ », « # », « ! »,« $ »,« ? ». Notez cependant que les noms de variables, dont la première lettre est « % », ont une signification particulière dans Scilab, comme nous le verrons dans le chapitre III-E, qui présente les variables mathématiques prédéfinies.
Scilab est sensible à la casse, ce qui signifie que les majuscules et minuscules sont considérées comme différentes par Scilab. Dans le script suivant, nous définissons les deux variables A et a et nous vérifions que ces deux variables sont considérées comme différentes par Scilab.
-->A = 2
A =
2.
-->a = 1
a =
1.
-->A
A =
2.
-->a
a =
1.III-C. Commentaires et continuations de lignes▲
Toute ligne qui commence par deux barres obliques « // » est considérée par Scilab comme un commentaire et est ignorée. Il n'est pas possible de commenter un bloc de lignes, comme avec les commentaires « /* … */ » en langage C.
Quand une instruction exécutable est trop longue pour être écrite sur une seule ligne, les lignes subséquentes sont appelées lignes de continuation. Dans Scilab, toute ligne qui se termine par deux points « .. » est considérée comme le début d'une nouvelle ligne de continuation. Dans l'exemple suivant, nous donnons des exemples de commentaires Scilab et de lignes de continuation :
-->// This is my comment.
-->x=1..
-->+2..
-->+3..
-->+4
x =
10.Voir le chapitre III-P pour plus de détails sur ce sujet.
III-D. Fonctions mathématiques élémentaires▲
Les tableaux suivants présentent une liste de fonctions mathématiques élémentaires.
| acos | acosd | acosh | acoshm | acosm | acot | acotd | acoth |
| acsc | acscd | acsch | asec | asecd | asech | asin | asind |
| asinh | asinhm | asinm | atan | atand | atanh | atanhm | atanm |
| cos | cosd | cosh | coshm | cosm | cotd | cotg | coth |
| cothm | csc | cscd | csch | sec | secd | sech | sin |
| sinc | sind | sinh | sinhm | sinm | tan | tand | tanh |
| tanhm | tanm |
| exp | expm | log | log10 | log1p | log2 | logm | max |
| maxi | min | mini | modulo | pmodulo | sign | signm | sqrt |
| sqrtm |
La plupart de ces fonctions prennent un argument d'entrée et renvoient un argument de sortie. Ces fonctions sont vectorisées dans le sens que leurs arguments d'entrée et de sortie sont des matrices. En conséquence, nous pouvons calculer des données avec des performances supérieures, sans aucune boucle.
Dans l'exemple suivant, nous utilisons les fonctions cos et sin et nous vérifions l'égalité cos(x)2+sin(x)2=1 :
-->x = cos(2)
x =
- 0.4161468
-->y = sin(2)
y =
0.9092974
-->x^2+y^2
ans =
1.III-E. Variables mathématiques prédéfinies▲
Dans Scilab, plusieurs variables mathématiques sont des variables prédéfinies, dont les noms commencent par un caractère pourcentage « % ». Les variables qui ont un sens mathématique sont résumées dans la liste suivante :
- %i : le nombre imaginaire i ;
- %e : le nombre d'Euler e ;
- %pi : la constante mathématique Pi.
Dans l'exemple suivant, nous utilisons la variable %pi pour vérifier l'égalité mathématique cos(x)2+sin(x)2=1 :
-->c=cos(%pi)
c =
- 1.
-->s=sin(%pi)
s =
1.225D-16
-->c^2+s^2
ans =
1.Le fait que la valeur calculée de sin(π) ne soit pas exactement égale à 0 est une conséquence du fait que Scilab stocke les nombres réels avec des nombres à virgule flottante, c'est-à-dire avec une précision limitée.
III-F. Booléens▲
Les variables booléennes peuvent stocker des valeurs « vrai » ou « faux ». Dans Scilab, la valeur « vrai » est écrite avec %t ou %T et la valeur « faux » est écrite avec %f ou %F. La liste suivante présente plusieurs opérateurs de comparaison disponibles dans Scilab :
- a&b : ET logique ;
- a|b : OU logique ;
- ~a : NON logique ;
- a==b : vrai si les deux expressions sont égales ;
- a~=b ou a<>b : vrai si les deux expressions sont différentes ;
- a<b : vrai si a est inférieur à b ;
- a>b : vrai si a est supérieur à b ;
- a<=b : vrai si a est inférieur ou égal à b ;
- a>=b : vrai si a est supérieur ou égal à b.
Ces opérateurs renvoient des valeurs booléennes et prennent comme arguments d'entrée tous les types de données de base (c'est-à-dire les nombres réels et complexes, les entiers et les chaînes). Les opérateurs de comparaison sont examinés au chapitre IV-N, où l'accent est mis sur la comparaison des matrices.
Dans l'exemple suivant, nous faisons quelques calculs algébriques avec les booléens de Scilab.
-->a=%T
a =
T
-->b = ( 0 == 1 )
b =
F
-->a&b
ans =
FIII-G. Les nombres complexes▲
Scilab fournit des nombres complexes, qui sont stockés sous forme de paires de nombres en virgule flottante. La variable prédéfinie %i représente le nombre mathématique imaginaire i qui satisfait i2=-1. Toutes les fonctions élémentaires précédemment présentées, comme sin, sont surchargées pour les nombres complexes. Cela signifie que si leur argument d'entrée est un nombre complexe, le résultat est un nombre complexe. La liste suivante présente les fonctions qui gèrent les nombres complexes.
- real : partie réelle ;
- imag : partie imaginaire ;
- imult : multiplication par i ;
- isreal : renvoie vrai si la variable n'a pas de partie complexe.
Dans l'exemple suivant, nous avons mis la variable x à 1+i, et nous effectuons plusieurs opérations de base sur celle-ci, telles que la récupération de ses parties réelles et imaginaires. Remarquez comment l'opérateur apostrophe, noté « ' », est utilisé pour calculer le conjugué d'un nombre complexe.
-->x= 1+%i
x =
1. + i
-->isreal(x)
ans =
F
-->x'
ans =
1. - i
-->y=1-%i
y =
1. - i
-->real(y)
ans =
1.
-->imag(y)
ans =
- 1.Nous avons enfin vérifié que l'égalité (1+i)(1-i)=1-i2=2 est vérifiée par Scilab.
-->x*y
ans =
2.III-H. Entiers▲
Nous pouvons créer différents types de variables entières avec Scilab. Les fonctions qui créent de tels entiers sont présentées dans la liste suivante :
- int8 ;
- int16 ;
- int32 ;
- uint8 ;
- uint16 ;
- uint32.
Dans cette section, nous examinons d'abord les fonctions de base d'entiers, qui sont associés à une certaine plage de valeurs. Puis, nous analysons la conversion entre les nombres entiers. Dans la dernière section, nous considérons le comportement d'entiers aux frontières et nous nous concentrons sur les problèmes de portabilité.
III-H-1. Vue d'ensemble des entiers▲
Il existe un lien direct entre le nombre de bits utilisés pour stocker un entier et la plage de valeurs que l'entier peut gérer. La plage d'une variable entière est fonction du nombre de ses bits :
- un entier signé sur n bits prend ses valeurs dans l'intervalle [-2n-1, 2n-1-1] ;
- un entier non signé sur n bits prend ses valeurs dans l'intervalle [0, 2n-1].
Par exemple, un entier signé sur 8 bits, tel que créé par la fonction int8, peut stocker des valeurs dans l'intervalle [-27, 27-1], ce qui simplifie en [-128, 127]. La correspondance entre le type de nombre entier et de la plage de valeurs correspondant est présentée sur la liste suivante :
- y=int8(x) : un entier signé sur 8 bits dans l'intervalle [-27, 27-1] soit [-128; 127] ;
- y=uint8(x) : un entier non signé sur 8 bits dans l'intervalle [0, 27-1] soit [0, 255] ;
- y=int16(x) : un entier signé sur 16 bits dans l'intervalle [-215, 215-1] soit [-32768, 32767] ;
- y=uint16(x) : un entier non signé sur 16 bits dans l'intervalle [0, 216-1] soit [0, 65535] ;
- y=int32(x) : un entier signé sur 32 bits dans l'intervalle [-231, 231-1] soit [-2147483648, 2147483647] ;
- y=uint32(x) : un entier non signé sur 32 bits dans l'intervalle [0, 232-1] soit [0, 4294967295].
Dans l'exemple suivant, nous vérifions qu'un entier non signé sur 32 bits a des valeurs à l'intérieur de l'intervalle [0, 232-1], soit [0, 4294967295] :
-->format(25)
-->n=32
n =
32.
-->2^n - 1
ans =
4294967295.
-->i = uint32(0)
i =
0
-->j=i-1
j =
4294967295
-->k = j+1
k =
0III-H-2. Les conversions entre entiers▲
Il y a des fonctions qui convertissent vers et à partir des types de données entier. Ces fonctions sont présentées dans la liste suivante :
- iconvert : conversion en représentation entière ;
- inttype : type des entiers.
La fonction inttype renseigne sur le type d'une variable entière. Selon le type, la fonction retourne une valeur correspondante, comme indiqué dans la liste suivante :
- 1 : entier signé sur 8 bits ;
- 2 : entier signé sur 16 bits ;
- 4 : entier signé sur 32 bits ;
- 11 : entier non signé sur 8 bits ;
- 12 : entier non signé sur 16 bits ;
- 14 : entier non signé sur 32 bits.
Lorsque deux nombres entiers sont ajoutés, les types des opérandes sont analysés : le type entier qui en résulte est le plus grand, de sorte que le résultat peut être stocké. Dans l'exemple qui suit, on crée un nombre entier i sur 8 bits (qui est associé à inttype=1) et un entier j sur 16 bits (qui est associé à inttype=2). Le résultat est stocké dans k, un entier signé sur 16 bits.
-->i = int8(1)
i =
1
-->inttype(i)
ans =
1.
-->j = int16(2)
j =
2
-->inttype(j)
ans =
2.
-->k = i+j
k =
3
-->inttype(k)
ans =
2.III-H-3. Entiers circulaires et problèmes de portabilité▲
Le comportement des entiers dans les limites du domaine mérite une analyse particulière, car il est différent d'un logiciel à un autre. Dans Scilab, le comportement est circulaire, c'est-à-dire que si un entier à la limite supérieure est incrémenté, la valeur suivante est à la limite inférieure. Un exemple de comportement circulaire est donné dans l'exemple suivant :
-->uint8(0+(-4:4))
ans =
252 253 254 255 0 1 2 3 4
-->uint8(2^8+(-4:4))
ans =
252 253 254 255 0 1 2 3 4
-->int8(2^7+(-4:4))
ans =
124 125 126 127 -128 -127 -126 -125 -124Ceci est en contraste avec d'autres logiciels mathématiques, comme Octave ou MATLAB. Dans ces logiciels, si un nombre entier est à la limite supérieure, le nombre entier reste à la limite supérieure. Dans l'exemple suivant sous Octave, nous exécutons les mêmes calculs que précédemment :
octave-3.2.4.exe:1> uint8(0+(-4:4))
ans =
0 0 0 0 0 1 2 3 4
octave-3.2.4.exe:5> uint8(2^8+(-4:4))
ans =
252 253 254 255 255 255 255 255 255
octave-3.2.4.exe:2> int8(2^7+(-4:4))
ans =
124 125 126 127 127 127 127 127 127Le comportement circulaire sous Scilab donne une plus grande souplesse dans le traitement des nombres entiers, puisque nous pouvons écrire des algorithmes avec moins d'instructions if . Mais ces algorithmes doivent être vérifiés, en particulier s'ils impliquent les limites de la plage des entiers. En outre, la traduction d'un script à partir d'un autre système de calcul dans Scilab peut conduire à des résultats différents.
III-I. Entiers en virgule flottante▲
Dans Scilab, la variable par défaut est le double numérique, c'est le nombre à virgule flottante codé sur 64 bits. Cela est vrai même si l'on écrit ce qui est mathématiquement un entier. Dans [11], Cleve Moler appelle ce nombre un « flint », un raccourci pour « floating point integer ». Dans la pratique, on peut en toute sécurité stocker des entiers dans l'intervalle [-252, 252] en double. Nous soulignons que, à condition que toutes les valeurs entières d'entrée, intermédiaires et de sortie soient strictement à l'intérieur de l'intervalle [-252, 252], les calculs avec des entiers sont exacts. Par exemple, dans l'exemple suivant, nous effectuons l'addition exacte de deux grands entiers qui restent dans l'intervalle « sûr » :
-->format(25)
-->a = 2^40 - 12
a =
1099511627764.
-->b = 2^45 + 3
b =
35184372088835.
-->c = a + b
c =
36283883716599.Au lieu de cela, quand on effectue des calculs en dehors de cet intervalle, on peut avoir des résultats inattendus. Dans l'exemple suivant, nous voyons que les additions impliquant des termes légèrement supérieurs à 253 ne produisent que des valeurs paires.
-->format(25)
-->(2^53 + (1:10))'
ans =
9007199254740992.
9007199254740994.
9007199254740996.
9007199254740996.
9007199254740996.
9007199254740998.
9007199254741000.
9007199254741000.
9007199254741000.
9007199254741002.Dans l'exemple suivant, on calcule 252 en utilisant l'entier 2 en virgule flottante dans le premier cas, et en utilisant l'entier 2 sur 16 bits dans le second cas. Dans le premier cas, aucun débordement ne se produit, même si le nombre est à la limite des nombres à virgule flottante sur 64 bits. Dans le second cas, le résultat est complètement faux, parce que le nombre 252 ne peut pas être représenté comme un entier sur 16 bits.
-->2^52
ans =
4503599627370496.
-->uint16(2^52)
ans =
0Dans le chapitre IV-O, nous analysons les problèmes qui se posent lorsque les indices concernés pour accéder aux éléments d'une matrice sont de type double.
III-J. La variable ans▲
Chaque fois que nous faisons un calcul et que nous ne stockons pas le résultat dans une variable de sortie, le résultat est stocké dans la variable par défaut ans. Une fois qu'elle est définie, nous pouvons utiliser cette variable comme n'importe quelle autre variable Scilab.
Dans l'exemple suivant, on calcule exp(3) de telle sorte que le résultat soit stocké dans la variable ans. Ensuite, nous utilisons son contenu comme une variable ordinaire.
-->exp(3)
ans =
20.08553692318766792368
-->t = log(ans)
t =
3.En général, la variable ans ne devrait être utilisée que dans une session interactive, afin de progresser dans le calcul sans définir une nouvelle variable. Par exemple, nous avons peut-être oublié de stocker le résultat d'un calcul intéressant et nous ne voulons pas recalculer le résultat. Ce pourrait être le cas après une longue série d'essais et d'erreurs, où nous avons expérimenté plusieurs façons d'obtenir le résultat sans réellement prendre soin de stocker le résultat. Dans ce cas interactif, utiliser ans peut faire économiser du temps homme (ou machine). Au lieu de cela, si nous développons un script utilisé d'une manière non interactive, c'est une mauvaise pratique que de compter sur la variable ans et nous devons stocker les résultats dans des variables normales.
III-K. Les chaînes de caractères▲
Les chaînes de caractères peuvent être stockées dans des variables, à condition qu'elles soient délimitées par des guillemets « " ». L'opération de concaténation est disponible à partir de l'opérateur « + ». Dans l'exemple suivant sous Scilab, nous définissons deux chaînes, puis nous les concaténons avec l'opérateur « + ».
-->x = "foo"
x =
foo
-->y = "bar"
y =
bar
-->x+y
ans =
foobarIl existe de nombreuses fonctions qui traitent les chaînes, y compris les expressions régulières. Nous ne donnerons pas plus de détails sur ce sujet dans le présent document.
III-L. Type dynamique des variables▲
Quand nous créons et gérons des variables, Scilab change le type de variable dynamiquement. Cela signifie que nous pouvons créer une valeur réelle, et ensuite mettre une variable de chaîne à l'intérieur, comme présenté dans l'exemple suivant :
-->x = 1
x =
1.
-->x+1
ans =
2.
-->x = "foo"
x =
foo
-->x+"bar"
ans =
foobarNous soulignons ici que Scilab n'est pas un langage typé, c'est-à-dire, que nous n'avons pas à déclarer le type d'une variable avant de définir son contenu. De plus, le type d'une variable peut changer au cours de la vie de la variable.
III-M. Notes et références▲
Le style de codage que nous avons présenté dans cette section et que nous allons utiliser dans le reste du document est la norme dans le contexte de Scilab. Ce style est basé sur des pratiques communes et sur le document [10], qui définit les conventions de code pour le langage de programmation Scilab. La convention définit la façon de définir de nouvelles fonctions (par exemple, leurs noms, le nom des arguments, etc.), le style d'indentation, les citations, la longueur des lignes, les indices des boucles, le nombre de déclarations par ligne, et de nombreux autres détails.
Dans le chapitre III-C, nous avons présenté la façon de définir des commentaires et des lignes de continuation et nous avons déclaré que toute ligne qui se termine par deux points est une ligne de continuation. En effet, l'interpréteur considère que toute ligne qui se termine par plus de deux points est une ligne de continuation. Cela signifie que nous pouvons utiliser les lignes de continuation avec trois points ou plus. Cette fonction est maintenue uniquement pour la compatibilité descendante, ne correspond plus au style de codage de Scilab et ne doit pas être utilisée dans de nouveaux scripts Scilab.
Dans le chapitre III-K, nous avons présenté les guillemets doubles « " » pour définir les chaînes. En effet, l'interpréteur peut également utiliser des chaînes définies avec des guillemets simples. Mais cela peut conduire à des bogues, car il pourrait y avoir une confusion avec l'opérateur de transposition (voir le chapitre IV-L). Cette fonctionnalité est conservée pour la compatibilité descendante et ne doit pas être utilisée dans de nouveaux scripts.
III-N. Exercices▲
Exercice III.1 - Ordre de priorité des opérateurs
Quels sont les résultats des calculs suivants (pensez-y avant d'essayer avec Scilab) ?
2 * 3 + 4
2 + 3 * 4
2 / 3 + 4
2 + 3 / 4Exercice III.2 - Parenthèses
Quels sont les résultats des calculs suivants (pensez-y avant d'essayer avec Scilab) ?
2 * (3 + 4)
(2 + 3) * 4
(2 + 3) / 4
3 / (2 + 4)Exercice III.3 - Exposants
Quels sont les résultats des calculs suivants (pensez-y avant d'essayer avec Scilab) ?
1.23456789d10
1.23456789e10
1.23456789e-5Exercice III.4 - Fonctions
Quels sont les résultats des calculs suivants (pensez-y avant d'essayer avec Scilab) ?
sqrt(4)
sqrt(9)
sqrt(-1)
sqrt(-2)
exp(1)
log(exp(2))
exp(log(2))
10^2
log10(10^2)
10^log10(2)
sign(2)
sign(-2)
sign(0)Exercice III.5 - Trigonométrie
Quels sont les résultats des calculs suivants (pensez-y avant d'essayer avec Scilab) ?
cos(0)
sin(0)
cos(%pi)
sin(%pi)
cos(%pi/4) - sin(%pi/4)IV. Les matrices▲
Dans le langage Scilab, les matrices jouent un rôle central. Dans cette section, nous introduisons les matrices sous Scilab et nous montrons comment créer des matrices et comment y accéder. Nous analysons également comment accéder aux éléments d'une matrice, soit élément par élément, soit par des opérations de plus haut niveau.
IV-A. Vue d'ensemble▲
Dans Scilab, le type de données de base est la matrice, qui est définie par :
- un nombre de lignes ;
- un nombre de colonnes ;
- un type de données.
Le type de données peut être réel, entier, booléen, chaîne et polynomial. Lorsque deux matrices ont le même nombre de lignes et de colonnes, nous disons que les deux matrices ont la même forme.
Dans Scilab, les vecteurs sont un cas particulier des matrices, où le nombre de lignes (ou le nombre de colonnes) est égal à 1. De simples variables scalaires n'existent pas dans Scilab : une variable scalaire est une matrice de une ligne et une colonne. C'est pourquoi, dans ce chapitre, lorsque nous analysons le comportement des matrices Scilab, il y a le même comportement pour les vecteurs de ligne ou de colonne (par exemple n×1 ou 1×n matrices) ainsi que des scalaires (c'est-à-dire matrices 1×1).
Il est juste de dire que Scilab a été conçu principalement pour les matrices de variables réelles, dans le but d'effectuer des opérations d'algèbre linéaire dans un langage de haut niveau.
De par sa conception, Scilab a été créé pour être en mesure d'effectuer les opérations matricielles aussi vite que possible. Le bloc de construction de cette fonctionnalité est que les matrices Scilab sont stockées dans une structure de données interne qui peut être géré au niveau de l'interpréteur. La plupart des opérations d'algèbre linéaire de base, telles que l'addition, la soustraction, la transposition ou le produit scalaire sont effectués par un code source optimisé et compilé. Ces opérations sont effectuées avec les opérateurs communs « + », « - », « * » et le single quote « ' », de sorte que, au niveau de Scilab, le code source est à la fois simple et rapide.
Grâce à ces opérateurs de haut niveau, la plupart des algorithmes matriciels n'ont pas besoin d'utiliser des boucles. En fait, un script Scilab qui effectue les mêmes opérations avec des boucles est généralement de dix à cent fois plus lent. Cette fonctionnalité de Scilab est connue sous le terme de vectorisation. Afin d'obtenir une mise en œuvre rapide d'un algorithme donné, le développeur Scilab doit toujours utiliser des opérations de haut niveau, de sorte que chaque instruction traite une matrice (ou un vecteur) au lieu d'un scalaire.
Des tâches plus complexes de l'algèbre linéaire, telles que la résolution de systèmes d'équations linéaires Ax=b, diverses décompositions (par exemple pivot partiel Gauss PA=LU), calculs de valeurs propres et de vecteurs propres, sont aussi effectués par des codes sources compilés et optimisés. Ces opérations sont effectuées par des opérateurs communs tels que la barre oblique « / » ou la barre oblique inverse « \ » ou encore avec des fonctions telles que spec, qui calcule les valeurs propres et vecteurs propres.
IV-B. Créer une matrice de valeurs réelles▲
Il existe une syntaxe simple et efficace pour créer une matrice avec des valeurs données. Ce qui suit est la liste des symboles utilisés pour définir une matrice :
- les crochets « [ » et « ] » marquent le début et la fin de la matrice ;
- les virgules « , » séparent les valeurs dans des colonnes différentes ;
- les points-virgules « ; » séparent les valeurs des lignes différentes.
La syntaxe suivante peut être utilisée pour définir une matrice, où les espaces sont facultatifs (mais rendent la ligne plus facile à lire) et « ... » indiquent des valeurs intermédiaires :
A = [a11, a12, ..., a1n; ... ; an1, an2, ..., ann].Dans l'exemple suivant, nous créons une matrice 2×3 de valeurs réelles :
-->A = [1 , 2 , 3 ; 4 , 5 , 6]
A =
1. 2. 3.
4. 5. 6.Une syntaxe simplifiée est disponible, qui ne nécessite pas d'utiliser les caractères virgule et point-virgule. Lors de la création d'une matrice, l'espace vide sépare les colonnes alors que la nouvelle ligne séparant les lignes, comme dans la syntaxe suivante :
A = [a11 a12 ... a1n
a21 a22 ... a2n
...
an1 an2 ... ann]Cela allège considérablement la gestion des matrices, comme dans l'exemple suivant :
-->A = [1 2 3
-->4 5 6]
A =
1. 2. 3.
4. 5. 6.La syntaxe précédente pour les matrices est utile dans les situations où les matrices doivent être écrites dans les fichiers de données, car elle simplifie la lecture humaine (et le contrôle) des valeurs dans le fichier, et simplifie la lecture de la matrice dans Scilab.
Plusieurs commandes Scilab créent des matrices à partir d'une taille donnée, c'est-à-dire à partir d'un nombre donné de lignes et de colonnes. Ces fonctions sont présentées dans la liste suivante :
- eye : matrice identité ;
- linspace : vecteur linéairement espacé ;
- ones : matrice composée de 1 ;
- zeros : matrice composée de 0 ;
- testmatrix : génération de quelques matrices particulières ;
- grand : générateur de nombre aléatoire ;
- rand : générateur de nombre aléatoire.
Les plus couramment utilisées sont eye, zeros et ones. Ces commandes prennent deux arguments d'entrée, le nombre de lignes et de colonnes de la matrice à générer.
-->A = ones(2,3)
A =
1. 1. 1.
1. 1. 1.IV-C. La matrice vide []▲
Une matrice vide peut être créée à l'aide de crochets vides, comme dans l'exemple suivant, où nous créons une matrice de dimension 0×0.
-->A = []
A =
[]Cette syntaxe supprime le contenu d'une matrice, de sorte que la mémoire associée est libérée.
-->A = ones(100,100);
-->A = []
A =
[]IV-D. matrices de requêtes▲
Les fonctions de la liste suivante questionnent ou mettent à jour une matrice :
- size : taille de l'objet ;
- matrix : redimensionne un vecteur ou une matrice à une différente taille ;
- resize_matrix : crée une nouvelle matrice avec une taille différente.
La fonction size renvoie deux arguments de sortie nr et nc, qui correspondent au nombre de lignes et au nombre de colonnes.
-->A = ones(2,3)
A =
1. 1. 1.
1. 1. 1.
-->[nr,nc] = size(A)
nc =
3.
nr =
2.La fonction size est une valeur pratique importante lorsque nous concevons une fonction, puisque le traitement que nous devons accomplir sur une matrice donnée peut dépendre de sa forme. Par exemple, pour calculer la norme d'une matrice donnée, différents algorithmes peuvent être utilisés en fonction de si la matrice est un vecteur colonne de taille nr×1 et nr>0, un vecteur ligne de taille 1×nc et nc>0, ou une matrice générale de taille nr×nc et nr,nc> 1.
La fonction size a également la syntaxe suivante :
nr = size( A , sel )qui ne reçoit que le nombre de lignes ou le nombre de colonnes et où sel peut prendre les valeurs suivantes :
- sel=1 ou sel="r" : retourne le nombre de lignes ;
- sel=2 ou sel="c" : retourne le nombre de colonnes ;
- sel="*" : renvoie le nombre total d'éléments, à savoir le nombre de colonnes multiplié par le nombre de rangées.
Dans l'exemple suivant, nous utilisons la fonction size afin de calculer le nombre total d'éléments d'une matrice.
-->A = ones(2,3)
A =
1. 1. 1.
1. 1. 1.
-->size(A,"*")
ans =
6.IV-E. Accès aux éléments d'une matrice▲
Il existe plusieurs méthodes pour accéder aux éléments d'une matrice A :
- toute la matrice, avec la syntaxe A ;
- élément par élément avec la syntaxe A(i,j) ;
- une gamme d'indices en indice avec l'opérateur deux-points « : ».
L'opérateur deux-points sera examiné dans la section suivante.
Pour faire un accès global à tous les éléments de la matrice, le nom de variable simple, par exemple A, peut être utilisé. Toutes les opérations d'algèbre élémentaires sont disponibles pour les matrices, telles que l'addition avec « + », la soustraction avec « - », à condition que les deux matrices soient de la même taille. Dans le script suivant, nous ajoutons tous les éléments de deux matrices.
-->A = ones(2,3)
A =
1. 1. 1.
1. 1. 1.
-->B = 2 * ones(2,3)
B =
2. 2. 2.
2. 2. 2.
-->A+B
ans =
3. 3. 3.
3. 3. 3.Un élément d'une matrice peut être consulté directement avec la syntaxe A(i,j), à condition que i et j soient des indices valables.
Nous soulignons que, par défaut, le premier indice d'une matrice est 1. Cela contraste avec d'autres langues, comme le langage C par exemple, où le premier indice est 0. Par exemple, supposons que A est une matrice de nr × nc, où nr est le nombre de lignes et nc est le nombre de colonnes. Par conséquent, la valeur de A(i,j) n'a de sens que si les indices i et j satisfont 1<=i<=n et j<=1<=nc. Si l'indice n'est pas valide, une erreur est générée, comme dans l'exemple suivant :
-->A = ones(2,3)
A =
1. 1. 1.
1. 1. 1.
-->A(1,1)
ans =
1.
-->A(12,1)
!--error 21
Index invalide.
-->A(0,1)
!--error 21
Index invalide.L'accès direct aux éléments de la matrice avec la syntaxe A(i,j) ne doit être utilisé que lorsqu'aucun autre niveau plus élevé de commandes Scilab ne peut être utilisé. En effet, Scilab offre de nombreuses fonctionnalités qui produisent des calculs simples et plus rapides, basés sur la vectorisation. Une de ces caractéristiques est l'opérateur deux-points « : », ce qui est très important dans des situations concrètes.
IV-F. L'opérateur deux-points « : »▲
La syntaxe la plus simple de l'opérateur deux-points est la suivante :
v = i: joù i est l'indice de départ et j est l'indice se terminant avec i<=j. Cela crée le vecteur v=(i, i+1, …, j). Dans l'exemple suivant, nous créons un vecteur d'indices 2 à 4 dans un communiqué.
-->v = 2:4
v =
2. 3. 4.La syntaxe complète configure l'incrément utilisé lors de la génération des indices, à savoir le pas. La syntaxe complète de l'opérateur « : » est :
v = i:s:joù i est l'indice de départ, j est l'indice de fin et s est le pas. Cette commande crée le vecteur v=(i, i+s, i+2s, …, i+ns) où n est le plus grand entier tel que i+ns<=j . Si s divise j-i, alors le dernier indice dans le vecteur d'indices est j. Dans d'autres cas, nous avons i+ns<j. Alors que dans la plupart des situations, le pas s est positif, il pourrait aussi être négatif.
Dans l'exemple suivant, nous créons un vecteur d'indices croissants de 3 à 10 avec un pas égal à 2.
-->v = 3:2:10
v =
3. 5. 7. 9.Notez que la dernière valeur dans le vecteur v est i+ns=9, qui est plus petit que j=10.
Dans l'exemple suivant, nous présentons deux exemples où le pas est négatif. Dans le premier cas, l'opérateur « : » génère des indices décroissants de 10 à 4. Dans le second exemple, l'opérateur « : » génère une matrice vide parce qu'il n'y a pas de valeur à la fois inférieure à 3 et supérieure à 10 en même temps.
-->v = 10:-2:3
v =
10. 8. 6. 4.
-->v = 3:-2:10
v =
[]Avec un vecteur d'indices, on peut accéder aux éléments d'une matrice dans une plage donnée, comme avec la syntaxe simplifiée suivante :
A(i:j,k:l)où i, j, k, l sont des indices de début et de fin. La syntaxe complète est :
A(i:s:j,k:t:l)où s et t sont les pas.
Par exemple, supposons que A soit une matrice 4×5, et que nous voulions pour accéder aux éléments ai,j pour i=1, 2 et j=3, 4. Avec le langage Scilab, cela peut être fait en une seule déclaration, en utilisant la syntaxe A(1:2,3:4), comme montré lors de l'exemple suivant :
-->A = testmatrix("hilb",5)
A =
25. - 300. 1050. - 1400. 630.
- 300. 4800. - 18900. 26880. - 12600.
1050. - 18900. 79380. - 117600. 56700.
- 1400. 26880. - 117600. 179200. - 88200.
630. - 12600. 56700. - 88200. 44100.
-->A(1:2,3:4)
ans =
1050. - 1400.
- 18900. 26880.Dans certaines circonstances, il peut arriver que les indices soient le résultat d'un calcul. Par exemple, l'algorithme peut être basé sur une boucle où les indices sont mis à jour régulièrement. Dans ces cas, la syntaxe :
A(vi,vj)où vi, vj sont des vecteurs d'indices, peut être utilisée pour désigner les éléments de A dont les indices sont les éléments de vi et vj. Cette syntaxe est illustrée dans l'exemple suivant :
-->A = testmatrix("hilb",5)
A =
25. - 300. 1050. - 1400. 630.
- 300. 4800. - 18900. 26880. - 12600.
1050. - 18900. 79380. - 117600. 56700.
- 1400. 26880. - 117600. 179200. - 88200.
630. - 12600. 56700. - 88200. 44100.
-->vi=1:2
vi =
1. 2.
-->vj=3:4
vj =
3. 4.
-->A(vi,vj)
ans =
1050. - 1400.
- 18900. 26880.
-->vi=vi+1
vi =
2. 3.
-->vj=vj+1
vj =
4. 5.
-->A(vi,vj)
ans =
26880. - 12600.
- 117600. 56700.Il y a beaucoup de variations sur cette syntaxe, et la liste suivante présente quelques-unes des combinaisons possibles :
- A : toute la matrice ;
- A(:,:) : toute la matrice ;
- A(i:j,k) : les éléments des rangées i à j, colonne k ;
- A(i,j:k) : les éléments de la ligne i, des colonnes j à k ;
- A(i,:) : la ligne i ;
- A(:,j) : la colonne j.
Par exemple, dans l'exemple qui suit, nous utilisons l'opérateur deux-points dans le but d'échanger deux lignes de la matrice A.
-->A = testmatrix("hilb",3)
A =
9. - 36. 30.
- 36. 192. - 180.
30. - 180. 180.
-->A([1 2],:) = A([2 1],:)
A =
- 36. 192. - 180.
9. - 36. 30.
30. - 180. 180.Nous pourrions également intervertir les colonnes de la matrice A avec l'instruction A(:,[3 1 2]).
Dans cette section, nous avons analysé plusieurs utilisations pratiques de l'opérateur deux-points. En effet, cet opérateur est utilisé dans beaucoup de scripts où la performance compte, car il accède à de nombreux éléments d'une matrice en une seule déclaration. Ceci est associé à la vectorisation de son exécution, un sujet qui est au cœur du langage Scilab et qui est passé en revue dans le présent document.
IV-G. La matrice eye▲
La fonction eye crée la matrice d'identité de la taille qui dépend du contexte. Son nom a été choisi à la place de « I » afin d'éviter la confusion avec un indice ou avec le nombre imaginaire.
Dans l'exemple suivant, on ajoute 3 aux éléments diagonaux de la matrice A.
-->A = ones(3,3)
A =
1. 1. 1.
1. 1. 1.
1. 1. 1.
-->B = A + 3*eye()
B =
4. 1. 1.
1. 4. 1.
1. 1. 4.Dans l'exemple suivant, nous définissons une matrice identité avec la fonction eye en fonction de la taille d'une matrice A donnée.
-->A = ones(2,2)
A =
1. 1.
1. 1.
-->B = eye(A)
B =
1. 0.
0. 1.Enfin, on peut utiliser la syntaxe eye(m,n) pour créer une matrice identité à m lignes et n colonnes.
IV-H. Matrices sont dynamiques▲
La taille d'une matrice peut augmenter ou diminuer dynamiquement. Ceci adapte la taille de la matrice aux données qu'elle contient.
Pensez à l'exemple suivant, où nous définissons une matrice 2×3.
-->A = [1 2 3; 4 5 6]
A =
1. 2. 3.
4. 5. 6.Dans l'exemple suivant, nous insérons la valeur 7 aux indices (3,1). Cela crée la troisième ligne dans la matrice, définit l'élément A(3,1) à 7 et remplit les autres valeurs de la ligne nouvellement créée par des zéros.
-->A(3,1) = 7
A =
1. 2. 3.
4. 5. 6.
7. 0. 0.L'exemple précédent a montré que les matrices peuvent se développer. Dans l'exemple suivant, nous voyons que nous pouvons aussi réduire la taille d'une matrice. Ceci est fait en utilisant l'opérateur de matrice vide « [] » afin de supprimer la troisième colonne.
-->A(:,3) = []
A =
1. 2.
4. 5.
7. 0.Nous pouvons aussi changer la forme de la matrice avec la fonction matrix. La fonction matrix remodèle une matrice source en une matrice cible avec une taille différente. La transformation est effectuée colonne par colonne, en empilant les éléments de la matrice source. Dans l'exemple suivant, nous remodelons la matrice A, qui dispose de 3×2=6 éléments dans un vecteur ligne avec 6 colonnes.
-->B = matrix(A,1,6)
B =
1. 4. 7. 2. 5. 0.IV-I. L'opérateur « $ »▲
Habituellement, nous utilisons un indice comme référence à partir du début d'une matrice. Par opposition, l'opérateur dollar « $ » références les éléments depuis la fin de la matrice. L'opérateur « $ » signifie « l'indice correspondant à la dernière » ligne ou une colonne, en fonction du contexte. La syntaxe est associée à une algèbre, de sorte que l'indice $-i correspond à l'indice l-1, où l est le nombre de lignes ou des colonnes correspondantes. Diverses utilisations de l'opérateur dollar sont présentées dans la liste suivante :
- A(i,$) : l'élément à la ligne i, à la colonne nc ;
- A($,j) : l'élément à la ligne nr, à la colonne j ;
- A($-i,$-j) : l'élément à la ligne nr-i, à la colonne nc-j.
Dans l'exemple suivant, nous considérons une matrice 3×3 et nous avons accès à l'élément A(2,1)=A(n-1,nc-2)=A($-1,$-2) parce que nr=3 et nc=3.
-->A=testmatrix("hilb",3)
A =
9. - 36. 30.
- 36. 192. - 180.
30. - 180. 180.
-->A($-1,$-2)
ans =
- 36.L'opérateur dollar « $ » ajoute dynamiquement des éléments à la fin des matrices. Dans l'exemple suivant, nous ajoutons une ligne à la fin de la matrice de Hilbert.
-->A($+1,:) = [1 2 3]
A =
9. - 36. 30.
- 36. 192. - 180.
30. - 180. 180.
1. 2. 3.L'opérateur « $ » est utilisé la plupart du temps dans le cadre de la déclaration « $+1 », ce qui ajoute à la fin d'une matrice. Cela peut être pratique, car elle évite la nécessité de mettre à jour le nombre de lignes ou de colonnes en continu, elle doit être utilisée avec prudence, uniquement dans les situations où le nombre de lignes ou de colonnes ne peut pas être connu à l'avance. La raison en est que l'interpréteur doit en interne réallouer de la mémoire pour la matrice entière et copier les anciennes valeurs vers la nouvelle destination. Cela peut conduire à des pénalités de performance et c'est pourquoi nous devons être en garde contre les mauvais usages de cet opérateur. Dans l'ensemble, la seule bonne utilisation de l'affirmation « $+1 » est quand nous ne savons pas à l'avance le nombre final de lignes ou de colonnes.
IV-J. Opérations de bas niveau▲
Tous les opérateurs communs de l'algèbre, tels que « + », « - », « * » et « / », sont disponibles avec des matrices réelles. Dans les sections suivantes, nous nous concentrons sur la signification exacte de ces opérateurs, de sorte que de nombreuses sources de confusion sont évitées.
Les règles pour les opérateurs « + » et « - » sont appliquées directement à partir de l'algèbre usuelle. Dans l'exemple suivant, nous ajoutons deux matrices 2×2.
-->A = [1 2
-->3 4]
A =
1. 2.
3. 4.
-->B = [5 6
-->7 8]
B =
5. 6.
7. 8.
-->A + B
ans =
6. 8.
10. 12.Lorsque l'on effectue une addition de deux matrices, si un opérande est une matrice 1×1 (à savoir, un scalaire), la valeur de ce scalaire est ajoutée à chaque élément de la seconde matrice. Cette fonction est représentée dans l'exemple suivant :
-->A = [1 2
-->3 4]
A =
1. 2.
3. 4.
-->A + 1
ans =
2. 3.
4. 5.L'addition n'est possible que si les deux matrices sont conformes à l'addition. Dans l'exemple suivant, nous essayons d'ajouter une matrice 2×3 avec une matrice 2×2 et nous vérifions que ce n'est pas possible.
-->A = [1 2
-->3 4]
A =
1. 2.
3. 4.
-->B = [1 2 3
-->4 5 6]
B =
1. 2. 3.
4. 5. 6.
-->A + B
!--error 8
Addition incohérente.Les opérateurs élémentaires qui sont disponibles pour les matrices sont présentés dans les listes suivantes :
|
|
Le langage Scilab fournit deux opérateurs de division, la division à droite « / » et la division à gauche « \ ». La division à droite « / » est telle que X=A/B=AB-1 est la solution de XB=A. La division gauche « \ » est telle que X = A\B = A-1B est la solution de AX=B. La division gauche A\B calcule la solution du problème associé au carré si A n'est pas une matrice carrée.
IV-K. Opérations élément par élément▲
Si un point « . » est écrit avant un opérateur, il est associé à un opérateur élément par élément, à savoir l'opération est effectuée élément par élément. Par exemple, avec l'opérateur de multiplication habituelle « * », le contenu de la matrice C=A*B est cij = Σk=1,n aikbkj. Avec la multiplication par l'opérateur élément par élément « .* » , le contenu de la matrice C=A.*B est cij=aijbij.
Dans l'exemple suivant, deux matrices sont multipliées par l'opérateur « * » et ensuite avec l'opérateur élément par élément « .* », afin que nous puissions vérifier que les résultats sont différents.
-->A = ones(2,2)
A =
1. 1.
1. 1.
-->B = 2 * ones(2,2)
B =
2. 2.
2. 2.
-->A*B
ans =
4. 4.
4. 4.
-->A.*B
ans =
2. 2.
2. 2.IV-L. Transposé conjuguée et non conjuguée▲
Il pourrait y avoir une certaine confusion lorsque le guillemet simple élément par élément « .' » et le guillemet simple normal « ' » sont utilisés sans une connaissance minutieuse de leurs définitions exactes. Avec une matrice de doubles contenant des valeurs réelles, l'opérateur apostrophe « ' » transpose seulement la matrice. Au lieu de cela, quand une matrice de doubles contenant des valeurs complexes est utilisée, l'apostrophe « ' » opérateur transpose et conjugue la matrice. Par conséquent, l'opération A=Z' produit une matrice avec des entrées Ajk=Xkj-iYkj, où i est le nombre imaginaire tel que i2=-1 et X et Y sont les parties réelle et imaginaire de la matrice Z. La citation élément par élément unique « . » transpose toujours sans la conjugaison de la matrice, qu'elle soit réelle ou complexe. Par conséquent, l'opération A=Z. produit une matrice avec des entrées Ajk=Xkj+iYkj.
Dans l'exemple suivant, une matrice non symétrique de doubles contenant des valeurs complexes est utilisée, de sorte que la différence entre les deux opérateurs est évidente.
-->A = [1 2;3 4] + %i * [5 6;7 8]
A =
1. + 5.i 2. + 6.i
3. + 7.i 4. + 8.i
-->A'
ans =
1. - 5.i 3. - 7.i
2. - 6.i 4. - 8.i
-->A.'
ans =
1. + 5.i 3. + 7.i
2. + 6.i 4. + 8.iDans l'exemple suivant, nous définissons une matrice non symétrique de doubles contenant des valeurs réelles et de voir que les résultats de « ' » et « .' » sont les mêmes dans ce cas particulier.
-->B = [1 2;3 4]
B =
1. 2.
3. 4.
-->B'
ans =
1. 3.
2. 4.
-->B.'
ans =
1. 3.
2. 4.De nombreux bogues sont créés en raison de cette confusion, de sorte qu'il est obligatoire de vous poser la question suivante : qu'advient-il si ma matrice est complexe ? Si la réponse est « Je veux transposer uniquement », alors l'opérateur élément par élément « .' » doit être utilisé.
IV-M. Multiplication de deux vecteurs▲
Soit u∈Rn un vecteur colonne et vT∈Rn un vecteur colonne. La matrice A=uvT possède des entrées Aij=uivj. Dans l'exemple suivant, on multiplie le vecteur u colonne par le vecteur ligne v et on stocke le résultat dans la variable A.
-->u = [1
-->2
-->3]
u =
1.
2.
3.
-->v = [4 5 6]
v =
4. 5. 6.
-->u*v
ans =
4. 5. 6.
8. 10. 12.
12. 15. 18.Cela pourrait conduire à une certaine confusion, car les manuels d'algèbre linéaire considèrent les vecteurs colonnes seulement. En général, nous désignons par u∈Rn un vecteur de colonne, de sorte que le vecteur ligne correspondant est désigné par uT. Dans la mise en œuvre associée Scilab, un vecteur ligne peut être directement stocké dans la variable u. Il pourrait également être une source de bogues, si le vecteur attendu est prévu pour être un vecteur ligne et est, en fait, un vecteur colonne. C'est pourquoi un algorithme qui ne fonctionne que sur un type particulier de matrice (vecteur ligne ou un vecteur colonne) devrait vérifier que le vecteur d'entrée a en effet la forme correspondante et générer une erreur si elle n'est pas.
IV-N. Comparaison de deux matrices réelles▲
La comparaison de deux matrices n'est possible que lorsque les matrices ont la même forme. Les opérateurs de comparaison présentés dans la liste suivante sont effectivement réalisés lorsque les arguments d'entrée A et B sont des matrices :
- A&B : ET logique ;
- A|B : OU logique ;
- ~A : NON logique ;
- A==B : vrai si les deux expressions sont égales ;
- A~=B ou A<>b : vrai si les deux expressions sont différentes ;
- A<B : vrai si A est inférieur à B ;
- A>B : vrai si A est supérieur à B ;
- A<=B : vrai si A est inférieur ou égal à B ;
- A>=B : vrai si A est supérieur ou égal à B.
Quand on compare deux matrices, le résultat est une matrice de booléens. Cette matrice peut ensuite être combinées avec des opérateurs tels que and et or, qui sont présentés dans la liste suivante :
- and(A,"r") : ET par ligne ;
- and(A,"c") : ET par colonne ;
- or(A,"r") : OU par ligne ;
- or(A,"c") : OU par colonne.
Les opérateurs habituels « & », « | » sont également disponibles pour les matrices, mais le ET et le OU permettent d'effectuer des opérations par ligne et par colonne.
Dans l'exemple suivant, nous créons une matrice A et le comparer avec le nombre 3. Notez que cette comparaison est valide parce que le nombre 3 est comparé élément par élément contre A. Nous créons ensuite une matrice B et de comparer les deux matrices A et B. Enfin, la fonction or est utilisée pour effectuer une comparaison par ligne afin que nous ayons les colonnes où une valeur dans la colonne de la matrice A est supérieure à une valeur dans la colonne de la matrice B.
-->A = [1 2 7
-->6 9 8]
A =
1. 2. 7.
6. 9. 8.
-->A>3
ans =
F F T
T T T
-->B = [ 4 5 6
-->7 8 9]
B =
4. 5. 6.
7. 8. 9.
-->A>B
ans =
F F T
F T F
-->or(A>B,"r")
ans =
F T TIV-O. Problèmes avec les nombres entiers en virgule flottante▲
Dans cette section, nous analysons les problèmes qui se posent lorsque l'on utilise des nombres entiers qui sont stockés sous forme de nombres à virgule flottante. Si elle est utilisée sans précaution, ces nombres peuvent conduire à des résultats désastreux, comme nous allons le voir.
Supposons que la matrice A soit une matrice carrée 2×2 :
-->A = testmatrix("hilb",2)
A =
4. - 6.
- 6. 12.Pour accéder à l'élément (2,1) de cette matrice, on peut utiliser un indice constant, tel que A(2,1), ce qui est sûr. Pour accéder à l'élément de la matrice, on peut utiliser des variables i et j et utiliser l'instruction A(i,j), comme dans l'exemple suivant :
-->i = 2
i =
2.
-->j = 1
j =
1.
-->A(i,j)
ans =
- 6.Dans l'exemple précédent, nous soulignons que les variables i et j sont doubles, c'est-à-dire des valeurs binaires à virgule flottante. C'est pourquoi l'instruction suivante est valide.
-->A( 2 , [1.0 1.1 1.5 1.9] )
ans =
- 6. - 6. - 6. - 6.L'exemple précédent montre que les valeurs à virgule flottante 1.0, 1.1, 1.5 et 1.9 sont toutes converties à l'entier 1, comme si la fonction floor avait été utilisée pour convertir le nombre à virgule flottante en un entier. En effet, la fonction floor retourne le nombre à virgule flottante stockant la partie entière du nombre à virgule flottante donné : dans un certain sens, il arrondit vers zéro. Par exemple, floor(1,0), floor(1,1), floor(1,5) et floor(1,9) renvoient tous 1.
C'est ce qui rend ce langage à la fois simple et efficace. Mais il peut aussi avoir des conséquences fâcheuses, ce qui conduit parfois à des résultats inattendus. Par exemple, considérons l'exemple suivant :
-->ones(1,1)
ans =
1.
-->ones(1,(1-0.9)*10)
ans =
[]Si les calculs sont effectués en arithmétique exacte, le résultat de (1-0.9)*10 est égal à 1. Au lieu de cela, l'expression ones(1,(1-0.9)*10) crée une matrice vide, parce que le résultat en virgule flottante de l'expression (1-0.9)*10 n'est pas exactement égal à 1. Dans l'exemple suivant, nous vérifions que la partie entière de (1-0.9)*10 est 0.
-->floor((1-0.9)*10)
ans =
0.En effet, le nombre décimal 0.9 ne peut pas être exactement représenté comme un nombre à virgule flottante double précision. Ce qui conduit à un arrondi, de telle sorte que la représentation en virgule flottante de 1-0.9 est légèrement plus petite que 0.1. Lorsque la multiplication (1-0.9)*10 est effectuée, le résultat en virgule flottante est donc légèrement plus petit que 1, tel que présenté à l'exemple suivant :
-->format(25)
-->1-0.9
ans =
0.0999999999999999777955
-->(1-0.9)*10
ans =
0.9999999999999997779554Ensuite, le nombre à virgule flottante 0.999999999999999 est considéré comme le nombre entier zéro, ce qui rend la fonction de ceux retourner une matrice vide. L'origine de ce problème est l'utilisation du nombre à virgule flottante binaire représentant 0.1, ce qui doit être utilisé avec prudence.
Il y a une façon de résoudre ce problème, en forçant la façon dont l'expression est arrondie à la valeur entière. Par exemple, nous pouvons utiliser la fonction round avant l'appel à la fonction ones.
-->n=round((1-0.9)*10);
-->ones(1,n)
ans =
1.En effet, la fonction round arrondit à l'entier le plus proche. Dans l'exemple suivant, on vérifie que n est exactement égal à 1.
-->n==1
ans =
TIl s'agit d'un effet pervers de l'utilisation de doubles qui crée ce genre de question. D'autre part, ce qui simplifie la plupart des expressions, de sorte que celle-ci s'avère être un atout majeur dans la plupart des situations. Nous pourrions ainsi blâmer l'interpréteur pour la conversion silencieuse d'un double avec une partie décimale en un nombre entier, sans générer (au minimum) un avertissement. Dans la pratique, il est toujours plus sûr d'arrondir un double avant l'appel d'une fonction qui attend réellement une valeur entière.
IV-P. Plus sur les fonctions élémentaires▲
Dans cette section, nous analysons plusieurs fonctions élémentaires, en particulier les fonctions trigonométriques en degrés, les fonctions logarithmes et les fonctions élémentaires basées sur les matrices.
Les fonctions trigonométriques telles que sin et cos sont fournies avec l'argument d'entrée classique en radians. Mais d'autres fonctions trigonométriques, telles que la fonction cosd par exemple, prennent un argument d'entrée en degrés. Cela signifie que, dans le sens mathématique tand(x) = tan(xπ/180). Ces fonctions peuvent être facilement identifiées car leur nom se termine par la lettre « d », par exemple, cosd, sind…. Le principal avantage pour les fonctions de base de degré primaire est qu'elles fournissent des résultats exacts lorsque leurs arguments ont des valeurs mathématiques spéciales, comme les multiples de 90 °. En effet, la mise en œuvre des fonctions de base de degré est basée sur une réduction d'argument qui est exacte pour des valeurs entières. Cela donne des résultats décimaux exacts pour des cas particuliers.
Dans l'exemple suivant, on calcule sin(π) et sind(180), qui sont mathématiquement égaux, mais sont associés à des résultats différents en virgule flottante.
-->sin(%pi)
ans =
1.225D-16
-->sind(180)
ans =
0.Le fait que sin(π) ne soit pas exactement zéro est dû à la précision limitée des nombres à virgule flottante. En effet, l'argument π est stocké en mémoire avec un nombre limité de chiffres significatifs, ce qui conduit à l'arrondir. Au lieu de cela, l'argument 180 est représenté exactement comme un nombre à virgule flottante, car il est un petit entier. Par conséquent, la valeur de sind(180) est calculée par la fonction sind comme le sin(0). Une fois de plus, le nombre zéro est exactement représenté par un nombre à virgule flottante. De plus, la fonction sin est représentée dans l'intervalle [-π/2, π/2] par un polynôme de la forme p(x)=x+x3q(x2), où q est un polynôme de degré faible. Par conséquent, nous obtenons sind(180)=sin(0)=0, ce qui est le résultat exact.
La fonction log calcule le logarithme népérien de l'argument d'entrée, qui est l'inverse de la fonction exp=ex, où e est le nombre d'Euler. Pour calculer la fonction logarithme pour d'autres bases, on peut utiliser les fonctions log10 et log2, associées avec des bases 10 et 2 respectivement. Dans l'exemple suivant, on calcule les valeurs des fonctions log, log10 et log2 pour certaines valeurs de x.
-->x = [exp(1) exp(2) 1 10 2^1 2^10]
x =
2.7182818 7.3890561 1. 10. 2. 1024.
-->[x' log(x') log10(x') log2(x')]
ans =
2.7182818 1. 0.4342945 1.442695
7.3890561 2. 0.8685890 2.8853901
1. 0. 0. 0.
10. 2.3025851 1. 3.3219281
2. 0.6931472 0.30103 1.
1024. 6.9314718 3.0103 10.La première colonne du tableau précédent contient différentes valeurs de x. La colonne numéro 2 contient des valeurs différentes de log(x), tandis que les colonnes 3 et 4 contiennent différentes valeurs de log10(x) et log2(x).
La plupart des fonctions opèrent élément par élément, qui est, étant donné une matrice d'entrée, appliquer la même fonction pour chaque entrée de la matrice. Cependant, certaines fonctions ont une signification particulière à l'égard de l'algèbre linéaire. Par exemple, la matrice d'une fonction exponentielle est définie par eX = ∑k-0,∞ 1/k! Xk, où X est une matrice carrée n×n. Pour calculer l'exponentielle d'une matrice, nous pouvons utiliser la fonction expm. De toute évidence, la fonction exponentielle élément par élément exp ne retourne pas le même résultat. Plus généralement, les fonctions qui ont une signification particulière en ce qui concerne les matrices ont un nom qui se termine par la lettre « m », par exemple expm, sinm, entre autres. Dans l'exemple suivant, nous définissons une matrice 2×2 contenant des multiples de π/2 et nous utilisons les fonctions sin et sinm.
-->A = [%pi/2 %pi; 2*%pi 3*%pi/2]
A =
1.5707963 3.1415927
6.2831853 4.712389
-->sin(A)
ans =
1. 1.225D-16
- 2.449D-16 - 1.
-->sinm(A)
ans =
- 0.3333333 0.6666667
1.3333333 0.3333333IV-Q. Fonctionnalités d'algèbre linéaire de niveau supérieur▲
Dans cette section, nous introduisons brièvement les fonctionnalités d'algèbre linéaire de niveau supérieur de Scilab.
Scilab dispose d'une bibliothèque d'algèbre linéaire complète, qui est capable de gérer à la fois des matrices denses et creuses. Un livre complet sur l'algèbre linéaire serait nécessaire pour faire une description des algorithmes fournis par Scilab dans ce domaine, et cela est évidemment hors de la portée de ce document. La liste suivante présente une liste des fonctions les plus courantes d'algèbre linéaire :
- chol : factorisation de Cholesky ;
- companion : matrice compagnon ;
- cond : conditionnement ;
- det : déterminant ;
- inv : matrice inverse ;
- linsolve : solveur d'équation linéaire ;
- lsq : problèmes linéaires des moindres carrés ;
- lu : facteurs LU de l'élimination gaussienne ;
- qr : décomposition QR ;
- rcond : conditionnement inverse ;
- spec : valeurs propres ;
- svd : décomposition en valeurs singulières ;
- testmatrix : une collection de matrices de test ;
- trace : trace.
IV-R. Exercices▲
Exercice IV.1 - Plus un
Créer le vecteur (x1+1, x2+1, x3+1, x4+1) avec les valeurs de x suivantes :
x = 1:4;Exercice IV.2 - Multiplication vectorisée
Créer le vecteur (x1y1, x2y2, x3y3, x4y4) avec les valeurs de x et y suivantes :
x = 1:4;
y = 5:8;Exercice IV.3 - Le point infâme
Analyser l'exemple suivant et expliquer pourquoi nous ne pourrions pas obtenir le résultat escompté.
-->expected=[1/2 1/3 1/4]
expected =
0.5 0.3333333 0.25
-->1./[2 3 4]
ans =
0.0689655
0.1034483
0.1379310Exercice IV.4 - Inversion vectorisée
Créer le vecteur (1/x1, 1/x2, 1/x3, 1/x4) avec les valeurs de x suivantes :
x = 1:4;Exercice IV.5 - Division vectorisée
Créer le vecteur (x1/y1, x2/y2, x3/y3, x4/y4) avec les valeurs de x et y suivantes :
x = 12*(6:9);
y = 1:4;Exercice IV.6 - Carré vectorisé
Créer le vecteur (x12, x22, x32, x42) avec x = 1, 2, 3, 4.
Exercice IV.7 - Sinus vectorisé
Créer le vecteur (sin(x1), sin(x2), …, sin(x10)) avec x un vecteur de dix valeurs choisies de façon linéaire dans l'intervalle [0, π].
Exercice IV.8 - Fonction vectorisée
Calculer les valeurs y=f(x) de la fonction f définie par l'équation f(x)=log10(r/10x+10x) (1) avec r=2.220.10-16 et x un vecteur de cent valeurs choisies de façon linéaire dans l'intervalle [-16, 0].
V. Boucle et branche ment▲
Dans cette section, nous décrivons comment faire des déclarations conditionnelles à l'aide de l'instruction if. Nous présentons l'instruction select qui crée des sélections plus complexes. Nous présentons les boucles for et while sous Scilab. Nous présentons enfin deux principaux outils pour gérer les boucles : break et continue.
V-A. L'instruction if▲
L'instruction if exécute une instruction si une condition est remplie. Le if utilise une variable booléenne pour effectuer son choix : si le booléen est vrai, alors l'instruction est exécutée. Une condition est fermée lorsque le mot end est atteint. Dans le script suivant, on affiche la chaîne « Hello ! » si la condition de %t, qui est toujours vraie, est satisfaite.
if ( %t ) then
disp("Hello !")
endLe script précédent produit :
Hello !Si la condition n'est pas remplie, l'instruction else effectue une instruction alternative, comme dans le script suivant :
if ( %f ) then
disp("Hello !")
else
disp("Goodbye !")
endLe script précédent produit :
Goodbye !Afin d'obtenir un booléen, un opérateur de comparaison peut être utilisé, par exemple, « == », « > »… ou toute autre fonction qui retourne un booléen. Dans l'exemple suivant, nous utilisons l'opérateur « == » pour afficher le message "Hello !".
i = 2
if ( i == 2 ) then
disp("Hello !")
else
disp("Goodbye !")
endIl est important de ne pas utiliser l'opérateur « = » dans la condition, c'est-à-dire qu'il ne faut pas utiliser l'instruction if (i = 2) then. C'est une erreur, car l'opérateur « = » définit une variable : il est différent de l'opérateur de comparaison « == ». En cas d'erreur, Scilab nous avertit que quelque chose de mal est arrivé.
-->i = 2
i =
2.
-->if (i = 2) then
Attention : Utilisation obsolète de '=' à la place de '=='.
!Lorsque nous devons combiner plusieurs conditions, l'expression elseif est utile. Dans le script suivant, nous combinons plusieurs déclarations elseif afin de gérer les différentes valeurs de l'entier i.
i = 2
if ( i == 1 ) then
disp("Hello !")
elseif ( i == 2 ) then
disp("Goodbye !")
elseif ( i == 3 ) then
disp("Tchao !")
else
disp("Au Revoir !")
endNous pouvons utiliser autant de déclarations elseif que nécessaire, ce qui crée des branches complexes selon les besoins. Mais s'il y a beaucoup de déclarations elseif nécessaires, cela peut impliquer qu'une instruction select doit être utilisée à la place.
V-B. L'instruction select▲
L'instruction select combine plusieurs branchements d'une manière claire et simple. En fonction de la valeur d'une variable, on effectue l'action correspondant au mot-clé case. Il peut y avoir autant de branches que nécessaire.
Dans le script suivant, nous voulons afficher une chaîne qui correspond à l'entier i donné.
i = 2
select i
case 1
disp("One")
case 2
disp("Two")
case 3
disp("Three")
else
disp("Other")
endLe script précédent affiche « Two », comme prévu.
La branche else est utilisée si toutes les conditions case précédentes sont fausses.
L'instruction else est facultative, mais est considérée comme une bonne pratique de programmation. En effet, même si le programmeur pense que le cas associé ne peut pas arriver, il peut encore exister un bogue dans la logique, de sorte que toutes les conditions sont fausses alors qu'elles ne devraient pas. Dans ce cas, si l'instruction else n'interrompt pas l'exécution, les instructions restantes dans le script seront exécutées. Cela peut conduire à des résultats inattendus. Dans le pire scénario, le script fonctionne toujours mais avec des résultats contradictoires. Le débogage de tels scripts est extrêmement difficile et peut conduire à une perte massive de temps.
Par conséquent, l'instruction else doit être incluse dans la plupart des séquences choisies. Afin de gérer ces événements imprévus, nous combinons souvent une instruction select avec la fonction error.
La fonction error génère une erreur associée au message donné. Quand une erreur est générée, l'exécution est interrompue et l'interpréteur quitte toutes ses fonctions. La pile d'exécution est donc effacée et le script s'arrête.
Dans le script suivant, on affiche un message en fonction de la valeur de la variable positive i. Si cette variable est négative, on génère une erreur.
i = -5;
select i
case 1
disp("One")
case 2
disp("Two")
case 3
disp("Three")
else
error( "Unexpected value of the parameter i" )
endLe script précédent produit la sortie suivante :
Unexpected value of the parameter iDans la pratique, quand on voit une instruction select sans le else correspondant, on peut se demander si le développeur a écrit ceci exprès ou basé sur l'hypothèse que cela n'arrivera jamais. La plupart du temps, cette hypothèse peut être discutée.
V-C. L'instruction for▲
L'instruction for réalise des boucles, c'est-à-dire qu'elle effectue une action donnée plusieurs fois. La plupart du temps, une boucle est réalisée sur des valeurs entières, qui vont d'un indice de départ à un indice de fin. Nous verrons, à la fin de cette section, que l'instruction for est en fait beaucoup plus générale, car elle peut permettre de boucler à travers les valeurs d'une matrice.
Dans le script suivant, on affiche la valeur de i, de 1 à 5 :
for i = 1 : 5
disp(i)
endLe script précédent produit la sortie suivante :
1.
2.
3.
4.
5.Dans l'exemple précédent, la boucle est effectuée sur une matrice de nombres à virgule flottante comportant des valeurs entières. En effet, nous avons utilisé l'opérateur deux-points « : » afin de produire le vecteur d'indices [1 2 3 4 5]. L'exemple suivant montre que l'instruction 1:5 génère toutes les valeurs entières requises dans un vecteur ligne.
-->i = 1:5
i =
1. 2. 3. 4. 5.Nous soulignons que, dans la boucle précédente, la matrice 1:5 est une matrice de doubles. Par conséquent, la variable i est également un double. Ce point sera examiné plus loin dans cette section, lorsque nous considérerons la forme générale d'une boucle for.
Nous pouvons utiliser une forme plus complète de l'opérateur « : » afin d'afficher les entiers impairs de 1 à 5. Pour ce faire, nous avons mis le pas de l'opérateur « : » à 2. Ceci est réalisé par le script Scilab suivant :
for i = 1 : 2 : 5
disp(i)
endLe script précédent produit la sortie suivante :
1.
3.
5.L'opérateur « : » peut être utilisé pour effectuer des boucles en arrière. Dans le script suivant, nous présentons les nombres de 5 à 1 :
for i = 5 : - 1 : 1
disp(i)
endLe script précédent produit la sortie suivante :
5.
4.
3.
2.
1.En effet, la déclaration 5:-1:1 produit tous les nombres entiers demandés :
-->i = 5:-1:1
i =
5. 4. 3. 2. 1.L'instruction for est beaucoup plus générale que ce que nous avons utilisé précédemment dans cette section. En effet, il navigue à travers les valeurs de nombreux types de données, y compris les matrices lignes et les listes. Lorsque nous effectuons une boucle for sur les éléments d'une matrice, cette matrice peut être une matrice de doubles, de chaînes, d'entiers ou de polynômes.
Dans l'exemple suivant, nous effectuons une boucle for sur les valeurs double d'une matrice ligne contenant (1.5, e, π).
v = [1.5 exp(1) %pi ];
for x = v
disp(x)
endLe script précédent produit la sortie suivante :
1.5
2.7182818
3.1415927Nous soulignons maintenant un point important à propos de l'instruction for. Chaque fois que nous utilisons une boucle for, nous devons nous demander si une instruction vectorisée pourrait effectuer le même calcul. Il peut y avoir un facteur dix à cent de performances entre les instructions vectorisées et une boucle for. La vectorisation permet d'effectuer des calculs rapides, même dans un environnement interprété comme Scilab. C'est pourquoi la boucle ne doit être utilisée que lorsqu'il n'y a pas d'autre moyen pour effectuer le même calcul avec des fonctions vectorielles.
V-D. L'instruction while▲
L'instruction while exécute une boucle tant qu'une expression booléenne est vraie. Au début de la boucle, si l'expression est vraie, les instructions dans le corps de la boucle sont exécutées. Lorsque l'expression est fausse (un événement qui doit se produire à certains moments), la boucle est terminée.
Dans le script suivant, nous calculons la somme des nombres i de 1 à 10 avec une instruction while.
s = 0
i = 1
while ( i <= 10 )
s = s + i
i = i + 1
endÀ la fin de l'algorithme, les valeurs des variables i et s sont les suivantes :
-->s
s =
55.
-->i
i =
11.Il doit être clair que l'exemple précédent est juste un exemple pour l'instruction while. Si nous voulions vraiment calculer la somme des nombres de 1 à 10, on devrait plutôt utiliser la fonction sum, comme dans l'exemple suivant :
-->sum(1:10)
ans =
55.L'instruction while a les mêmes problèmes de performance que l'instruction for. C'est pourquoi les instructions vectorisées doivent être considérées d'abord, avant d'essayer de concevoir un algorithme basé sur une boucle while.
V-E. Les instructions break et continue▲
L'instruction break interrompt une boucle. Habituellement, nous utilisons cette instruction dans les boucles où, une fois une condition remplie, les boucles ne doivent pas être poursuivies. Dans l'exemple suivant, nous utilisons l'instruction break afin de calculer la somme des entiers de 1 à 10. Lorsque la variable i est supérieure à 10, la boucle est interrompue.
s = 0
i = 1
while ( %t )
if ( i > 10 ) then
break
end
s = s + i
i = i + 1
endÀ la fin de l'algorithme, les valeurs des variables i et s sont les suivantes :
-->s
s =
55.
-->i
i =
11.L'instruction continue fait aller l'interpréteur à l'itération suivante, de sorte que les déclarations contenues dans le corps de la boucle ne sont pas exécutées cette fois. Lorsque l'instruction continue est exécutée, Scilab ignore les autres déclarations et va directement à l'instruction while ou for et évalue l'itération suivante.
Dans l'exemple suivant, nous calculons la somme s=1+3+5+7+9=25. La fonction modulo(i,2) renvoie 0 si le nombre i est pair. Dans cette situation, le script passe à la prochaine boucle.
s = 0
i = 0
while ( i< 10 )
i = i + 1
if ( modulo(i,2) == 0 ) then
continue
end
s = s + i
endSi le script précédent est exécuté, les valeurs finales des variables i et s sont les suivantes :
-->s
s =
25.
-->i
i =
10.À titre d'exemple de calcul vectoriel, l'algorithme précédent peut être réalisé en un seul appel de fonction. En effet, le script suivant utilise la fonction sum, combinée avec l'opérateur deux-points « : » et produit le même résultat.
s = sum(1:2:10);Le script précédent a deux avantages principaux par rapport l'algorithme basé sur while :Claude Leloup 2013-03-14T19:58:55La liste est ouverte par un deux-pointsChaque item se termine par un point-virgule quel que soit le signe de ponctuation éventuellement inclus dans l'item. Le dernier item se termine par un point. Quant à savoir s'il faut une minuscule initiale ou une majuscule initiale, cela dépend du signe (éventuel) qui introduit l'item. S'il contient un point (« 1. », « A. »…) il faut une majuscule, sinon une minuscule (pas de signe, un tiret, « 1 », « a », une puce…).
- Le calcul fait usage d'un langage de plus haut niveau, ce qui est plus facile à comprendre pour les êtres humains ;
- Avec de grandes matrices, le calcul de la somme à l'aide de sum sera beaucoup plus rapide que l'algorithme basé sur while.
C'est pourquoi une analyse minutieuse doit être effectuée avant l'élaboration d'un algorithme basé sur une boucle while.
VI. Les fonctions▲
Dans cette section, nous présentons les fonctions Scilab. Nous analysons la façon de définir une nouvelle fonction et la méthode pour la charger dans Scilab. Nous présentons comment créer et charger une bibliothèque, qui est une collection de fonctions. Nous présentons également comment gérer les arguments d'entrée et de sortie. Enfin, nous présentons comment déboguer une fonction en utilisant l'instruction pause.
VI-A. Vue d'ensemble▲
Rassembler les différentes étapes dans une fonction réutilisable est l'une des tâches les plus courantes d'un développeur Scilab. La séquence d'appel la plus simple d'une fonction est la suivante :
outvar = myfunction ( invar )où :
- myfunction est le nom de la fonction ;
- invar est le nom des arguments d'entrée ;
- outvar est le nom des arguments de sortie.
Les valeurs des paramètres d'entrée ne sont pas modifiées par la fonction, tandis que les valeurs des paramètres de sortie sont réellement modifiées par la fonction.
Nous avons en effet déjà rencontré plusieurs fonctions dans ce document. La fonction sin, dans l'instruction y=sin(x), prend l'argument d'entrée x et renvoie le résultat dans l'argument de sortie y. Dans le vocabulaire de Scilab, les arguments en entrée sont appelés « right hand side » et les arguments de sortie sont appelés « left hand side ».
Les fonctions peuvent avoir un nombre quelconque de paramètres d'entrée et de sortie de telle sorte que la syntaxe de la fonction qui a un nombre fixe d'arguments est la suivante :
[o1, ..., on] = MyFunction (i1, ..., in)Les arguments d'entrée et de sortie sont séparés par des virgules « , ». Notez que les arguments d'entrée sont entourés de parenthèses ouvrantes et fermantes, tandis que les arguments de sortie sont entourés de crochets ouvrants et fermants.
Dans l'exemple suivant, nous montrons comment calculer la décomposition LU de la matrice de Hilbert. L'exemple montre comment créer une matrice avec la fonction testmatrix, qui prend deux arguments en entrée et renvoie une matrice. Ensuite, nous utilisons la fonction lu, qui prend un argument et retourne deux ou trois arguments en fonction des variables de sortie prévues. Si le troisième argument P est fourni, la matrice de permutation est retournée.
-->A = testmatrix("hilb",2)
A =
4. - 6.
- 6. 12.
-->[L,U] = lu(A)
U =
- 6. 12.
0. 2.
L =
- 0.6666667 1.
1. 0.
-->[L,U,P] = lu(A)
P =
0. 1.
1. 0.
U =
- 6. 12.
0. 2.
L =
1. 0.
- 0.6666667 1.Notez que le comportement de la fonction lu change effectivement lorsque trois arguments de sortie sont prévus : les deux lignes de la matrice L ont été échangées. Plus précisément, lorsque deux arguments de sortie sont prévus, la décomposition A=LU est fournie (la déclaration AL*U vérifie cela). Lorsque trois arguments de sortie sont prévus, les permutations sont effectuées de telle sorte que la décomposition PA=LU est fournie (la déclaration P*AL*U peut être utilisée pour vérifier). En effet, quand deux arguments de sortie sont prévus, les permutations sont appliquées sur la matrice L. Cela signifie que la fonction lu sait combien d'arguments d'entrée et de sortie lui sont fournis, et change son algorithme en conséquence. Nous ne présentons pas dans ce document comment assurer cette fonction, c'est-à-dire un nombre variable d'entrée ou de sortie arguments. Mais nous devons garder à l'esprit que cela est possible dans le langage Scilab.
Les commandes fournies par Scilab pour gérer les fonctions sont présentées dans la liste suivante :
- function : ouvre la définition d'une fonction ;
- endfunction : ferme la définition d'une fonction ;
- argn : nombre d'entrées/sorties lors de l'appel d'une fonction ;
- varargin : nombre d'arguments dans une liste d'arguments d'entrée ;
- varargout : nombre d'arguments dans une liste d'arguments de sortie ;
- fun2string : génère la définition ASCII d'une fonction Scilab ;
- get_function_path : renvoie le chemin source d'une fonction de bibliothèque ;
- getd : renvoie toutes les fonctions définies dans un répertoire ;
- head_comments : affiche les commentaires d'entête d'une fonction Scilab ;
- listfunctions : propriétés de toutes les fonctions dans l'espace de travail ;
- macrovar : les variables de la fonction.
Dans les sections suivantes, nous allons présenter quelques-unes des commandes les plus couramment utilisées.
VI-B. Définir une fonction▲
Pour définir une nouvelle fonction, nous utilisons les mots-clés Scilab function et endfunction. Dans l'exemple suivant, nous définissons la fonction myfunction, qui prend l'argument d'entrée x, qui le multiplie par 2, et renvoie la valeur de l'argument de sortie y.
function y = myfunction ( x )
y = 2 * x
endfunctionL'instruction function y = myfunction (x) est l'entête de la fonction tandis que l'instruction y=2*x est le corps de la fonction. Le corps d'une fonction peut contenir une, deux ou plusieurs instructions.
Il existe au moins trois possibilités pour définir la fonction précédente dans Scilab :
- la première solution consiste à taper directement le script dans la console en mode interactif. Notez que, une fois que l'instruction « function y = myfunction (x) » a été rédigée et la touche Entrée est tapée, Scilab crée une nouvelle ligne dans la console, en attendant que le corps de la fonction soit saisi. Lorsque l'instruction « endfunction » est tapée dans la console, Scilab retourne à son mode d'édition normal ;
- une autre solution est disponible lorsque le code source de la fonction est fourni dans un fichier. C'est le cas le plus fréquent, puisque les fonctions sont généralement assez longues et compliquées. Nous pouvons tout simplement copier et coller la définition de la fonction dans la console. Lorsque la définition de la fonction est courte (typiquement, une douzaine de lignes de code source), cette façon de faire est très pratique. Avec l'éditeur, ce qui est très facile, grâce à la fonction « Load into Scilab » ;
- nous pouvons également utiliser la fonction exec. Considérons un système Windows où la fonction précédente est écrite dans le fichier « examples-functions.sce », dans le répertoire « C:\myscripts ». L'exemple suivant montre l'utilisation de exec pour charger la fonction précédente ;Sélectionnez
-->exec("C:\myscripts\examples-functions.sce") --> function y = myfunction ( x ) --> y = 2 * x --> endfunction - la fonction exec exécute le contenu du fichier comme s'il avait été écrit de manière interactive dans la console et affiche les différentes instructions Scilab, ligne après ligne. Le fichier peut contenir une grande quantité de code source, de sorte que la sortie peut être très longue et inutile. Dans ces situations, nous ajoutons le caractère point-virgule « ; » à la fin de la ligne. C'est ce qui est réalisé par la commande « Execute File into Scilab » de l'éditeur.
-->exec("C:\myscripts\examples-functions.sce" );Une fois qu'une fonction est définie, elle peut être utilisée comme s'il s'agissait d'une autre fonction Scilab.
-->exec("C:\myscripts\examples-functions.sce");
-->y = myfunction ( 3 )
y =
6.Notez que la fonction précédente définit la valeur de l'argument de sortie y avec l'instruction y=2*x. Ceci est obligatoire. Pour le voir, on définit dans le script suivant une fonction qui définit la variable z, mais pas l'argument y de sortie.
function y = myfunction ( x )
z = 2 * x
endfunctionDans l'exemple suivant, nous essayons d'utiliser notre fonction avec l'argument d'entrée x=1.
--> myfunction ( 1 )
!-- error 4
Variable non définie : y
at line 4 of function myfunction called by :
myfunction ( 1 )En effet, l'interpréteur nous indique que la variable de sortie y n'a pas été définie. Lorsque nous faisons un calcul, nous avons souvent besoin de plus d'une fonction pour effectuer toutes les étapes de l'algorithme. Par exemple, considérons la situation où nous avons besoin d'optimiser un système. Dans ce cas, on peut utiliser un algorithme fourni par Scilab, disons optim par exemple. Tout d'abord, nous définissons la fonction de coût qui doit être optimisée, selon le format attendu par optim. Deuxièmement, nous définissons un driver, qui appelle la fonction optim avec les arguments requis. Au moins deux fonctions sont utilisées dans ce schéma simple. Dans la pratique, un calcul complet nécessite souvent une douzaine de fonctions, ou plus. Dans ce cas, nous pouvons recueillir nos fonctions dans une bibliothèque et c'est le sujet du prochain chapitre.
VI-C. Bibliothèques de fonctions▲
Une bibliothèque de fonctions est un ensemble de fonctions définies dans le langage Scilab et stockées dans un ensemble de fichiers.
Quand un ensemble de fonctions est simple et ne contient aucune aide ou aucun code source dans un langage compilé comme le C/C++ ou Fortran, une bibliothèque est un moyen très efficace de procéder. Au lieu de cela, lorsque nous concevons un composant Scilab avec les tests unitaires, les pages d'aide et de scripts de démonstration, nous développons un module. Élaborer un module est à la fois simple et efficace, mais nécessite une connaissance plus avancée de Scilab. De plus, les modules sont basés sur des bibliothèques de fonctions, de sorte que la compréhension des premières nous fait maîtriser ces dernières. Les modules ne seront pas décrits dans le présent document. Pourtant, dans de nombreuses situations pratiques, les bibliothèques de fonctions permettent une gestion efficace des collections simples de fonctions et c'est pourquoi nous décrivons ce système ici.
Dans cette section, nous décrivons une bibliothèque très simple et nous montrons comment la charger automatiquement au démarrage de Scilab.
Faisons un bref aperçu du processus de création et d'utilisation d'une bibliothèque. Nous supposons que l'on nous donne un ensemble de fichiers .sci contenant des fonctions.
- Nous créons une version binaire des scripts contenant les fonctions. La fonction genlib génère des versions binaires des scripts, ainsi que les fichiers d'indexation supplémentaires.
- Nous chargeons la bibliothèque dans Scilab. La fonction lib charge une bibliothèque stockée dans un répertoire particulier.
Avant d'analyser un exemple, prenons quelques règles générales qui doivent être suivies lors de la conception d'une bibliothèque de fonctions. Ces règles seront ensuite examinées dans l'exemple suivant.
Les noms de fichiers contenant des définitions de fonction doit se terminer par l'extension .sci. Ce n'est pas obligatoire, mais permet d'identifier les scripts Scilab sur un disque dur.
Plusieurs fonctions peuvent être stockées dans chaque fichier .sci, mais seule la première sera disponible depuis l'extérieur du fichier. En effet, la première fonction du fichier est considérée comme la seule fonction publique, tandis que les autres fonctions sont (implicitement) des fonctions privées.
Le nom du fichier .sci doit être le même que le nom de la première fonction dans le fichier. Par exemple, si la fonction doit être nommée « myfun », le fichier contenant cette fonction doit être « myfun.sci ». Ceci est obligatoire pour que la fonction genlib fasse le travail correctement.
Les fonctions qui gèrent les bibliothèques sont présentées dans la liste suivante :
- genlib : création d'une bibliothèque de fonctions dans un répertoire donné ;
- lib : définition d'une bibliothèque.
Nous allons maintenant donner un petit exemple d'une bibliothèque particulière et donner quelques détails sur la façon de réellement commencer. Supposons que nous utilisions un système Windows et que le répertoire « C:\samplelib » contienne deux fichiers :
- C:\samplelib\function1.sci :Sélectionnez
function y = function1 ( x ) y = 1 * function1_support ( x ) endfunction function y = function1_support ( x ) y = 3 * x endfunction - C:\samplelib\function2.sci :
function y = function2 ( x )
y = 2 * x
endfunctionDans l'exemple suivant, nous générons les fichiers binaires avec la fonction genlib, qui prend comme premier argument une chaîne associée avec le nom de la bibliothèque, et prend comme second argument le nom du répertoire contenant les fichiers. Notez que seules les fonctions function1 et function2 sont accessibles publiquement : la fonction function1_support peut être utilisée à l'intérieur de la bibliothèque, mais ne peut pas être utilisée à l'extérieur.
--> genlib("mylibrary","C:\samplelib")
--> mylibrary
mylibrary =
Emplacement des fichiers de fonctions : C:\samplelib\.
function1 function2La fonction genlib génère les fichiers suivants dans le répertoire « C:\samplelib » :
- function1.bin : la version binaire du script function1.sci ;
- function2.bin : la version binaire du script function2.sci ;
- lib : une version binaire de la bibliothèque ;
- names : un fichier texte contenant la liste des fonctions de la bibliothèque.
Les fichiers binaires *.bin et le fichier lib sont portables dans le sens où ils fonctionnent aussi bien sous Windows, Linux ou Mac. Une fois la fonction genlib exécutée, les deux fonctions sont immédiatement disponibles, comme indiqué dans l'exemple suivant :
--> function1(3)
ans =
9.
--> function2(3)
ans =
6.En pratique, cependant, nous ne générerons pas la bibliothèque à chaque fois que cela est nécessaire. Une fois que la bibliothèque est prête, nous tenons à charger la bibliothèque directement. Cela se fait avec la fonction lib, qui prend comme premier argument le nom du répertoire contenant la bibliothèque et renvoie la bibliothèque, comme dans l'exemple suivant :
--> mylibrary = lib("C:\samplelib\")
ans =
Emplacement des fichiers de fonctions : C:\samplelib\.
function1 function2S'il y a beaucoup de bibliothèques, il pourrait être gênant pour charger manuellement toutes les bibliothèques au démarrage. Dans la pratique, la déclaration lib peut être écrite une fois pour toutes, dans Scilab fichier de démarrage, de sorte que la bibliothèque est immédiatement disponible au démarrage. Le répertoire de démarrage associé à une installation particulière Scilab est stocké dans le SCIHOME variable, tel que présenté à la séance suivante, par exemple sur Windows.
-->SCIHOME
SCIHOME =
C:\Users\username\AppData\Roaming\Scilab\scilab-5.3.1Dans le répertoire associé à la variable SCIHOME, le fichier de démarrage est « .scilab ». Le fichier de démarrage est automatiquement lu par Scilab au démarrage. Il doit être un script Scilab régulier (il peut contenir des commentaires valides). Pour rendre notre bibliothèque disponible au démarrage, nous écrivons simplement les lignes suivantes dans notre fichier « .scilab » :
// Load my favorite library.
mylibrary = lib("C:\samplelib")Avec ce fichier de démarrage, les fonctions définies dans la bibliothèque sont disponibles directement au démarrage de Scilab.
VI-D. Gestion des arguments de sortie▲
Dans cette section, nous présentons les différentes façons de gérer les arguments de sortie. Une fonction peut avoir zéro ou plusieurs paramètres d'entrée et/ou de sortie. Dans le cas le plus simple, le nombre de paramètres d'entrée et de sortie est prédéfini et utiliser une telle fonction est facile. Mais, comme nous allons le voir, même une fonction aussi simple peut être appelée de différentes façons.
Supposons que la fonction simplef soit définie avec deux arguments d'entrée et deux arguments de sortie, comme suit :
function [y1 , y2] = simplef ( x1 , x2 )
y1 = 2 * x1
y2 = 3 * x2
endfunctionEn fait, le nombre d'arguments de sortie d'une telle fonction peut être 0, 1 ou 2. Quand il n'y a pas d'argument de sortie, la valeur du premier argument de sortie est stockée dans la variable ans. Nous pouvons également définir la variable y1 seulement. Enfin, on peut utiliser tous les arguments de sortie, comme prévu. L'exemple qui suit présente l'ensemble de ces séquences d'appel.
--> simplef(1,2)
ans =
2.
-->y1 = simplef(1,2)
y1 =
2.
-->[y1 ,y2] = simplef(1,2)
y2 =
6.
y1 =
2.Nous avons vu que la façon la plus simple de définir des fonctions permet déjà de gérer un nombre variable d'arguments de sortie. Il existe un moyen encore plus souple de la gestion d'un nombre variable d'arguments d'entrée et de sortie, en fonction des variables argn, varargin et varargout. Ce sujet plus avancé ne sera pas détaillé dans ce document.
VI-E. Les niveaux dans la pile d'exécution▲
De toute évidence, les appels de fonctions peuvent être imbriqués, c'est-à-dire qu'une fonction f peut appeler une fonction g, qui à son tour appelle une fonction h et ainsi de suite. Lorsque Scilab commence, les variables qui sont définies sont de portée globale. Lorsque nous sommes dans une fonction qui est appelée à partir de la portée globale, nous sommes d'un niveau vers le bas dans la pile des appels. Lorsque les appels ultérieurs de fonctions imbriquées, le niveau de courant dans la pile d'exécution est égal au nombre d'appels déjà emboîtés. Les fonctions présentées dans la liste suivante renseignent sur l'état de la pile d'exécution :
- whereami : affiche l'arbre courant d'instruction appelante ;
- where : obtient l'arbre courant d'instruction appelante.
Dans l'exemple suivant, nous définissons trois fonctions qui réclament une de l'autre et nous utilisons la fonction whereami pour afficher l'arborescence d'instruction en cours d'appel.
function y = fmain ( x )
y = 2 * flevel1 ( x )
endfunction
function y = flevel1 ( x )
y = 2 * flevel2 ( x )
endfunction
function y = flevel2 ( x )
y = 2 * x
whereami ()
endfunctionLorsque nous appelons cette fonction fmain, la sortie suivante est produite. Comme nous pouvons le voir, les trois niveaux de la pile d'appelpile d'exécution sont affichés et associés à la fonction correspondante.
-->fmain(1)
whereami appelée à la ligne 3 de la macro flevel2
flevel2 appelée à la ligne 2 de la macro flevel1
flevel1 appelée à la ligne 2 de la macro fmain
ans =
8.Dans l'exemple précédent, les différents niveaux d'appel sont les suivants :
- niveau 0 : le niveau global ;
- niveau -1 : le corps de la fonction fmain ;
- niveau -2 : le corps de la fonction flevel1 ;
- niveau -3 : le corps de la fonction flevel2.
Ces niveaux d'appel sont affichés dans l'invite de la console quand on débogue une fonction interactivement avec l'instruction pause ou avec des points d'arrêt.
VI-F. L'instruction return▲
À l'intérieur du corps d'une fonction, l'instruction return arrête immédiatement la fonction, c'est-à-dire qu'il quitte immédiatement la fonction en cours. Cette déclaration peut être utilisée dans les cas où le reste de l'algorithme n'est pas nécessaire.
La fonction suivante calcule la somme des nombres entiers de istart à iend. En situation régulière, elle utilise la fonction sum pour effectuer son travail. Mais si la variable istart est négative ou si la condition istart<=iend n'est pas satisfaite, la variable de sortie y est mise à 0 et la fonction revient immédiatement.
function y = mysum ( istart , iend )
if ( istart < 0 ) then
y = 0
return
end
if ( iend < istart ) then
y = 0
return
end
y = sum ( istart : iend )
endfunctionL'exemple suivant vérifie que l'instruction return est utilisée correctement par la fonction mysum.
-->mysum(1,5)
ans =
15.
-->mysum(-1,5)
ans =
0.
-->mysum(2,1)
ans =
0.Certains développeurs indiquent que l'utilisation de plusieurs instructions return dans une fonction est généralement une mauvaise pratique. En effet, il faut tenir compte de la difficulté augmentée de débogage d'une telle fonction, parce que l'algorithme peut soudainement quitter le corps de la fonction. L'utilisateur peut être confus au sujet de ce qui a exactement causé la fonction retourne.
C'est pourquoi, dans la pratique, l'instruction return doit être utilisée avec précaution, et certainement pas dans toutes les fonctions. La règle à suivre est que la fonction doit retourner uniquement à sa dernière ligne. Cependant, dans des situations particulières, utiliser return peut effectivement grandement simplifier l'algorithme, tandis qu'en évitant return, il faudrait écrire beaucoup de code source inutile.
VI-G. Fonctions de débogage avec pause▲
Dans cette section, nous présentons les méthodes de débogage simples qui fixent les bogues les plus simples d'une manière pratique et efficace. Plus précisément, nous présentons les instructions pause, resume et abort, qui sont détaillées dans la liste suivante :
- pause : attent une saisie interactive de l'utilisateur ;
- resume : reprend l'exécution et copie des variables locales ;
- abort : interrompt l'évaluation.
Une session Scilab consiste généralement à définir de nouveaux algorithmes par la création de nouvelles fonctions. Il arrive souvent qu'une erreur de syntaxe ou une erreur dans l'algorithme produise un résultat erroné.
Considérons le problème, la somme des nombres entiers de istart à iend. Encore une fois, cet exemple simple est choisi pour des fins de démonstration, puisque la fonction sum, l'effectue directement.
La fonction mysum suivante contient un bogue : le second argument « foo » passé à la fonction sum n'a pas de sens dans ce contexte.
function y = mysum ( istart , iend )
y = sum ( iend : istart , "foo" )
endfunctionL'exemple suivant montre ce qui arrive quand on utilise la fonction mysum.
-->mysum(1,10)
!--error 44
Argument 2 erroné.
at line 2 of function mysum called by :
mysum(1,10)Afin de trouver le problème de manière interactive, nous plaçons une instruction pause à l'intérieur du corps de la fonction.
function y = mysum ( istart , iend )
pause
y = sum ( iend : istart , "foo" )
endfunctionNous appelons maintenant la fonction mysum de nouveau avec les mêmes arguments d'entrée.
-->mysum(1,10)
Saisissez 'resume' ou 'abort' pour revenir au niveau de prompt standard.
-1->Nous sommes maintenant placés interactivement dans le corps de la fonction mysum. L'invite « -1 --> » indique que la pile d'exécution courante est au niveau -1. On peut vérifier la valeur des variables istart et iend en tapant simplement leur nom dans la console.
-1->istart
istart =
1.
-1->iend
iend =
10.Afin de progresser dans notre fonction, nous pouvons copier et coller les instructions et voir ce qui se passe de manière interactive, comme dans l'exemple suivant :
-1->y = sum ( iend : istart , "foo" )
y = sum ( iend : istart , "foo" )
!--error 44
Argument 2 erroné.Nous pouvons voir que l'appel à la fonction sum ne se comporte pas comme nous pourrions nous y attendre. L'argument d'entrée « foo » est certainement un bogue : on l'enlève.
-1->y = sum ( iend : istart )
y =
0.Après la première révision, l'appel à la fonction sum est syntaxiquement correct. Mais le résultat n'est toujours pas correct, puisque le résultat attendu dans ce cas est de 55. Nous voyons que les variables istart et iend ont été échangées. Nous corrigeons l'appel de fonction et nous vérifions que la version corrigée se comporte comme prévu :
-1->y = sum ( istart : iend )
y =
55.Le résultat est désormais correct. Pour revenir au niveau zéro, nous utilisons maintenant l'instruction abort, ce qui interrompt la séquence et retourne immédiatement au niveau global.
-1->abort
-->L'invite « --> » confirme que nous sommes maintenant de retour au niveau zéro dans la pile des appels. Nous corrigeons la définition de la fonction, qui devient :
fonction y = mySum (istart, iend)
pause
y = somme (istart: iend)
endfunctionAfin de vérifier notre correction de bogue, nous appelons à nouveau la fonction.
-->mysum(1,10)
-1->Nous sommes maintenant confiants quant à notre code, de sorte que nous utilisons l'instruction resume, ce qui permet d'exécuter le code Scilab comme d'habitude.
-1->resume
ans =
55Le résultat est correct. Tout ce que nous avons à faire est de retirer l'instruction pause de la définition de la fonction.
function y = mysum ( istart , iend )
y = sum ( istart : iend )
endfunctionDans cette section, nous avons vu que, en combinaison, les instructions pause, resume et abort sont un moyen très efficace pour déboguer une fonction interactivement. En fait, notre exemple est très simple et la méthode que nous avons présentée peut paraître trop simple pour être pratique. Ce n'est pas le cas. Dans la pratique, la déclaration de pause s'est avérée être un moyen très rapide pour trouver et corriger les bogues, même dans des situations très complexes.
VII. Graphiques▲
La production des tracés et des graphiques est une tâche très commune pour l'analyse des données et la création de rapports. Scilab offre plusieurs façons de créer et de personnaliser différents types de tracés et de graphiques. Dans cette section, nous présentons la façon de créer des graphes 2D et les tracés de contours. Ensuite, nous personnalisons le titre et la légende de nos graphiques. Nous exportons finalement les tracés afin de pouvoir les utiliser dans un rapport.
VII-A. Vue d'ensemble▲
Scilab peut produire de nombreux types de tracés 2D et 3D. Il peut créer des graphiques x-y avec la fonction plot, des tracés de contour avec la fonction contour, des graphiques en 3D avec la fonction surf, des histogrammes avec la fonction histplot et de nombreux autres types de tracés. Les fonctions de tracé les plus couramment utilisées sont présentées dans la liste suivante :
- plot : tracé 2D ;
- surf : tracé 3D ;
- contour: tracé de contour ;
- pie : camembert ;
- histplot : histogramme ;
- bar : diagramme à barres ;
- barh : diagramme à barres horizontales ;
- hist3d : histogramme 3D ;
- polarplot : tracé en coordonnées polaires ;
- Matplot: tracé 2D d'une matrice en utilisant des couleurs ;
- Sgrayplot : tracé 2D lissé d'une surface en utilisant des couleurs ;
- grayplot : tracé 2D d'une surface en utilisant des couleurs.
Pour obtenir un exemple d'un graphique 3D, nous pouvons simplement taper l'instruction surf() dans la console Scilab.
-->surf()Lors de la création d'un tracé, nous utilisons plusieurs fonctions afin de créer des données ou pour configurer le tracé. Les fonctions présentées dans la liste suivante seront utilisées dans les exemples de ce chapitre :
- linspace : vecteur linéairement espacé ;
- feval : évalue une fonction sur une grille ;
- legend : configure la légende du tracé actuel ;
- title : configure le titre du tracé en cours ;
- xtitle : configure le titre et les légendes du tracé en cours.
VII-B. Tracé 2D▲
Dans cette section, nous présentons la façon de produire une représentation x-y simple. Nous insistons sur l'utilisation des fonctions vectorielles, qui produisent des matrices de données dans un appel de fonction.
Nous commençons par définir la fonction qui doit être tracée. La fonction myquadratic élève l'argument d'entrée x au carré avec l'opérateur « ^ ».
function f = myquadratic ( x )
f = x^2
endfunctionNous pouvons utiliser la fonction linspace afin de produire cinquante valeurs dans l'intervalle [1, 10].
xdata = linspace ( 1 , 10 , 50 );La variable xdata contient maintenant un vecteur ligne avec cinquante éléments, où la première valeur est égale à 1 et la dernière valeur est égale à 10. Nous pouvons passer cette variable à la fonction myquadratic et obtenir la valeur de fonction à des points donnés.
ydata = myquadratic (xdata);On obtient ainsi le vecteur ligne ydata, qui contient cinquante éléments. Nous avons finalement utiliser la fonction plot de sorte que les données sont affichées comme une représentation x-y (xdata, ydata).
Notez que nous aurions pu produire le même tracé sans générer le tableau intermédiaire ydata. En effet, le second argument d'entrée de la fonction plot peut être une fonction, comme dans l'exemple suivant :
plot (xdata, myquadratic)Lorsque le nombre de points à gérer est important, utiliser directement des fonctions préserve une grande quantité d'espace mémoire, car cela évite la génération du vecteur intermédiaire ydata.
VII-C. Tracés de contours▲
Dans cette section, nous présentons les tracés de contour d'une fonction de plusieurs variables et nous utilisons la fonction contour. Ce type de graphique est souvent utilisé dans le contexte d'optimisation numérique, car il trace des fonctions de deux variables d'une manière qui montre l'emplacement de l'optimum.
Supposons que l'on nous donne la fonction f à n variables f(x)=f(x1, …, xn) et x∈Rn. Pour un α∈R donné, l'équation f(x)=α (2) définit une surface dans l'espace dimensionnelle (n+1) Rn+1.
Lorsque n=2, les points z=f(x1,x2) représentent une surface dans l'espace à trois dimensions (x1, x2, z)∈R3. Cela dessine les tracés de contours de la fonction de coût, comme nous allons le voir. Pour n>3, cependant, ces tracés ne sont pas disponibles. Une solution possible dans ce cas consiste à sélectionner deux paramètres significatifs et d'en tirer un tracé de contour avec ces paramètres variables (uniquement).
La fonction Scilab contour trace les contours d'une fonction f. La fonction contour a la syntaxe suivante :
contour (x, y, z, nz)où :
- x (resp. y) est un vecteur ligne de x (resp. y) des valeurs dont la taille n1 (resp. n2) ;
- z est une matrice réelle de taille (n1, n2), contenant les valeurs de la fonction ou une fonction Scilab qui définit la surface z=f(x,y) ;
- nz les valeurs des niveaux ou le nombre de niveaux.
Dans l'exemple suivant, nous utilisons une forme simple de la fonction contour, où la fonction myquadratic est passée comme argument d'entrée. La fonction myquadratic prend deux arguments d'entrées x1 et x2 et renvoie f(x1,x2)=x12+x22. La fonction linspace est utilisée pour générer des vecteurs de données de telle sorte que la fonction est analysée dans la plage [-1, 1]2.
function f = myquadratic2arg ( x1 , x2 )
f = x1 **2 + x2 **2;
endfunction
xdata = linspace ( -1 , 1 , 100 );
ydata = linspace ( -1 , 1 , 100 );
contour ( xdata , ydata , myquadratic2arg , 10)On obtient ainsi le tracé de contour présenté dans la Figure 44.
Dans la pratique, il peut arriver que notre fonction ait l'entête z = myfunction (x), où la variable d'entrée x est un vecteur ligne. Le problème est qu'il n'y a qu'un seul argument d'entrée unique, au lieu des deux arguments requis par la fonction contour. Il y a deux possibilités pour résoudre ce petit problème :
- fournir les données de la fonction contour en faisant deux boucles imbriquées ;
- fournir les données de la fonction contour en utilisant feval ;
- définir une nouvelle fonction qui appelle la première.
Ces trois solutions sont présentées dans cette section. Le premier objectif est de permettre au lecteur de choisir la méthode qui convient le mieux à la situation. Le deuxième objectif est de montrer que les questions de performances peuvent être évitées si une utilisation cohérente des fonctions fournies par Scilab est faite.
Dans l'exemple naïf suivant, nous définissons la fonction myquadratic1arg, qui prend un vecteur comme argument d'entrée unique. Ensuite, nous effectuons deux boucles imbriquées pour calculer la matrice zdata, qui contient les valeurs de z. Les valeurs z sont calculées pour toutes les combinaisons de points (x(i),y(j))∈R2, pour i=1, 2, …, nx et j=1, 2, …, ny, où nx et ny sont le nombre de points dans les coordonnées x et y. En fin de compte, nous appelons la fonction contour, avec la liste des niveaux requis (au lieu du numéro précédent de niveau). Ceci nous donne exactement les niveaux que nous voulons, au lieu de laisser Scilab calculer les niveaux automatiquement.
function f = myquadratic1arg ( x )
f = x (1)**2 + x (2)**2;
endfunction
xdata = linspace ( -1 , 1 , 100 );
ydata = linspace ( -1 , 1 , 100 );
// Caution ! Two nested loops , this is bad.
for i = 1: length ( xdata )
for j = 1: length ( ydata )
x = [ xdata (i) ydata (j)].';
zdata ( i , j ) = myquadratic1arg ( x );
end
end
contour ( xdata , ydata , zdata , [0.1 0.3 0.5 0.7])Le tracé de contour est présenté à la figure 45.
Le script précédent fonctionne parfaitement. Pourtant, il n'est pas efficace car il utilise deux boucles imbriquées, ce qui devrait être évité dans Scilab pour des raisons de performances. Un autre problème est que nous devons stocker la matrice zdata, ce qui pourrait consommer beaucoup d'espace mémoire lorsque le nombre de points est grand. Cette méthode doit être évitée car elle est une mauvaise utilisation des fonctionnalités offertes par Scilab.
Dans le script suivant, nous utilisons la fonction feval, qui évalue une fonction sur une grille de valeurs et renvoie les données calculées. La grille générée est composée de toutes les combinaisons de points (x(i),y(j))∈R2. Nous supposons ici qu'il n'y a aucune possibilité de modifier la fonction myquadratic1argqui prend un argument d'entrée. Par conséquent, nous créons une fonction intermédiaire myquadratic3, qui prend deux arguments d'entrée. Une fois cela fait, nous passons l'argument myquadratic3 à la fonction feval et nous générons la matrice zdata.
function f = myquadratic1arg ( x )
f = x (1)**2 + x (2)**2;
endfunction
function f = myquadratic3 ( x1 , x2 )
f = myquadratic1arg ( [x1 x2] )
endfunction
xdata = linspace ( -1 , 1 , 100 );
ydata = linspace ( -1 , 1 , 100 );
zdata = feval ( xdata , ydata , myquadratic3 );
contour ( xdata , ydata , zdata , [0.1 0.3 0.5 0.7])Le script précédent produit, bien sûr, exactement le même tracé que précédemment. Cette méthode doit être évitée autant que possible, car cela nécessite le stockage de la matrice zdata, qui a une taille de 100×100.
Enfin, il existe une troisième voie pour créer un tracé. Dans l'exemple suivant, nous utilisons la même fonction intermédiaire myquadratic3 comme précédemment, mais nous la transmettons directement à la fonction contour.
function f = myquadratic1arg ( x )
f = x (1)**2 + x (2)**2;
endfunction
function f = myquadratic3 ( x1 , x2 )
f = myquadratic1arg ( [x1 x2] )
endfunction
xdata = linspace ( -1 , 1 , 100 );
ydata = linspace ( -1 , 1 , 100 );
contour ( xdata , ydata , myquadratic3 , [0.1 0.3 0.5 0.7])Le script précédent produit, bien sûr, exactement le même tracé que précédemment. L'avantage majeur est que nous n'avons pas créé la matrice zdata.
Nous avons brièvement décrit la façon de produire de simples tracés 2D. Nous sommes maintenant intéressés par la configuration du tracé, de sorte que les titres, les axes et les légendes correspondent à nos données.
VII-D. Titres, axes et des légendes▲
Dans cette section, nous présentons les fonctionnalités graphiques de Scilab qui configurent le titre, les axes et les légendes d'un graphique x-y.
Dans l'exemple suivant, nous définissons une fonction quadratique et la traçons avec la fonction plot.
function f = myquadratic ( x )
f = x.^2
endfunction
xdata = linspace ( 1 , 10 , 50 );
ydata = myquadratic ( xdata );
plot ( xdata , ydata )Nous obtenons à nouveau le tracé qui est présenté à la Figure 43.
Le système de graphiques Scilab est basé sur les identifiants graphiques. Les identifiants graphiques fournissent un accès orienté objet aux champs d'une entité graphique. La mise en page graphique est décomposée en sous-objets, tels que la ligne associée à la courbe, les axes x et y, le titre, les légendes, etc. Chaque objet peut être à son tour décomposé en d'autres objets si nécessaire. Chaque objet graphique est associé à un ensemble de propriétés, telles que la largeur ou la couleur de la ligne de la courbe. Ces propriétés peuvent être interrogées et configurées simplement pour en obtenir ou définir leurs valeurs, comme toutes autres variables Scilab. Gérer des identifiants est facile et très efficace.
Mais la plupart des configurations de tracé les plus élémentaires peuvent être faites par des appels de fonctions simples et, dans cette section, nous allons nous concentrer sur ces fonctions de base.
Dans le script suivant, nous utilisons la fonction title afin de configurer le titre de notre tracé :
title("My title");Nous pouvons souhaiter configurer les axes de notre tracé également. Pour ce faire, nous utilisons la fonction xtitle dans le script suivant :
xtitle ( "My title" , "X axis" , "Y axis" );La figure 46 présente le tracé produit.
Il peut arriver que l'on souhaite comparer deux ensembles de données sur le même tracé 2D, un ensemble de données x et deux ensembles de données y. Dans le script suivant, nous définissons les deux fonctions f(x)=x2 et f(x)=2x2 et nous traçons les données sur le même graphique x-y. En outre, nous utilisons les options « +- » et « o- » de la fonction plot, afin de pouvoir distinguer les deux courbes f(x)=x2 et f(x)=2x2.
function f = myquadratic ( x )
f = x^2
endfunction
function f = myquadratic2 ( x )
f = 2 * x^2
endfunction
xdata = linspace ( 1 , 10 , 50 );
ydata = myquadratic ( xdata );
plot ( xdata , ydata , "+-" )
ydata2 = myquadratic2 ( xdata );
plot ( xdata , ydata2 , "o-" )
xtitle ( "My title " , "X axis " , "Y axis " );En outre, il faut configurer une légende afin de savoir quelle courbe est associée à f(x)=x2 et quelle courbe est associée à f(x)=2x2. Pour ce faire, nous utilisons la fonction legend pour afficher la légende associée à chaque courbe.
legend ("x^2", "2x^2");La figure 47 montre le tracé produit.
Nous savons maintenant comment créer un graphique, et comment le configurer. Si le tracé est suffisamment intéressant, il peut être utile de le mettre dans un rapport. Pour ce faire, nous pouvons exporter le graphique dans un fichier, ce qui est l'objet du chapitre suivant.
VII-E. Export▲
Dans cette section, nous présentons des moyens d'exporter des tracés dans des fichiers, de manière interactive ou automatique avec des fonctions Scilab.
Scilab peut exporter des graphiques dans les formats vectoriel et bitmap présentés dans les deux listes suivantes.
Format vectoriel :
- xs2png : export en PNG ;
- xs2pdf : export en PDF ;
- xs2svg : export en SVG ;
- xs2eps : export en PostScript encapsulé ;
- xs2ps : export en PostScript ;
- xs2emf : export en EMF (uniquement pour Windows).
Format bitmap :
- xs2fig : export en FIG ;
- xs2gif : export en GIF ;
- xs2jpg : export en JPG ;
- xs2bmp : export en BMP ;
- xs2ppm : export en PPM.
Dès qu'un tracé est réalisé, nous pouvons exporter son contenu dans un fichier, interactivement en utilisant le menu « File > Export to… » de la fenêtre graphique. Nous pouvons alors définir le nom du fichier et son type.
Nous pouvons également utiliser les fonctions xs2*, présentées dans la liste précédente. Toutes ces fonctions sont basées sur la même séquence d'appel :
xs2png ( window_number , filename )où window_number est le numéro de la fenêtre graphique et filename est le nom du fichier à exporter. Par exemple, l'exemple suivant exporte le tracé qui est dans la fenêtre graphique numéro 0, qui est la fenêtre graphique par défaut, dans le fichier foo.png.
xs2png ( 0 , "foo.png" )Si nous voulons produire des documents de qualité supérieure, les formats vectoriels sont préférés. Par exemple, les documents LATEX peuvent utiliser des tracés Scilab exportés en fichiers PDF afin d'améliorer leur lisibilité, quelle que soit la taille du document.
VIII. Notes et références▲
Il y a un certain nombre de sujets qui n'ont pas été présentés dans ce document. Nous espérons néanmoins que c'est un bon point de départ pour l'utilisation de Scilab et que l'apprentissage de ces sujets spécifiques ne devrait pas être un problème. Nous avons déjà mentionné un certain nombre d'autres sources de documentation à cet effet au début de ce document.
Les lecteurs francophones peuvent être intéressés par [5], où une bonne introduction est donnée sur la façon de créer et d'interfacer une bibliothèque existante, comment utiliser Scilab pour calculer la solution d'une équation différentielle ordinaire, comment utiliser Scicos et bien d'autres sujets. Le même contenu est présenté en anglais dans [3]. Les lecteurs anglophones devraient être intéressés par [4], qui donne une meilleure vue d'ensemble de Scicos. Ces livres sont d'un grand intérêt, mais sont plutôt obsolètes car ils ont été écrits principalement à partir d'anciennes versions de Scilab.
Des lectures complémentaires peuvent être obtenues à partir du site internet de Scilab [13], dans la section documentation.
IX. Remerciements▲
Je tiens à remercier Claude Gomez, Vincent Couvert, Cornet Allan et Serge Steer qui m'ont laissé partager leurs commentaires sur ce document. Je suis également reconnaissant à Julie Paul qui m'a aidé lors de la rédaction de ce document. Un grand merci à Sylvestre Ledru, qui a clarifié plusieurs points sur les processus d'installation de Scilab, et le système ATOMS. Remerciements également exprimés à Artem Glebov et Jason Nicholson pour la relecture de ce document. Je remercie Rokach Ihor pour ses commentaires sur ce document.
X. Réponses aux exercices▲
X-A. Réponses pour le chapitre I▲
Solution de l'exercice I.1 - Installation de Scilab
Installez la version actuelle du logiciel Scilab sur votre système : au moment où ce document est écrit, c'est Scilab v5.3. L'installation de Scilab est très facile, puisque les binaires sont fournis. Les figures suivantes présentent les étapes nécessaires pour installer Scilab v5.1.1 sous Windows.
Solution de l'exercice I.2 - L'aide en ligne : derivative
La fonction derivative calcule la dérivée d'une fonction numérique. Le but de cet exercice est de trouver la page d'aide correspondante, par divers moyens. Nous ouvrons le navigateur d'aide de la console, dans le menu « ? > Help Browser ». Nous sélectionnons maintenant le volet de recherche sur la gauche, et nous saisissons « derivative », puis nous appuyons sur la touche Entrée. Toutes les pages contenant le mot « derivative » sont affichées. La première est la page d'aide que nous recherchons. Nous pouvons également utiliser l'aide fournie sur le site internet de Scilab : http://www.scilab.org/product/man.
Nous utilisons l'outil « Rechercher » de notre navigateur préféré et recherchons le mot derivative. Nous avons successivement trouver les fonctions : diff, bsplin3val, derivative, dérivat et dlgamma. La page recherchée est la suivante : http://www.scilab.org/product/man/derivative.html.
Nous avons finalement utilisé la console pour trouver de l'aide :
help derivativeLa figure suivante présente la page d'aide pour derivative.
X-B. Réponses pour le chapitre II▲
Solution de l'exercice II.1 - La console
Tapez la commande suivante dans la console :
atomsMaintenant, tapez sur la touche de tabulation. Qu'est-ce qui se passe ? Nous voyons que toutes les fonctions dont le nom commence par les lettres « atoms » sont affichées, tel que présenté dans la figure suivante :
Maintenant, tapez la lettre « I », puis tapez à nouveau sur la touche de tabulation. Qu'est-ce qui se passe ? Nous voyons que toutes les fonctions dont le nom commence par les lettres « atomsI » sont affichées, tel que présenté dans la figure suivante :
Solution de l'exercice II.2 - Utiliser exec
La variable SCI contient le nom du répertoire d'installation de Scilab. L'instruction SCI+"/modules" crée une chaîne qui est la concaténation du nom du répertoire Scilab et de la chaîne « /modules », comme indiqué dans l'exemple suivant :
-->SCI+"/modules"
ans =
C:/PROGRA~1/SCILAB~1.0-B/modulesPar conséquent, lorsque nous effectuons la commande ls(SCI+"/modules"), Scilab affiche la liste des fichiers dans le sous-répertoire « modules » de Scilab.
-->ls(SCI+"/modules")
ans =
!xml !
! !
!xcos !
! !
!windows_tools !
! !
[...]L'exécution du script de démonstration « contourf.dem.sce » produit le graphique présenté dans la figure suivante :
Nous avons mis le nom du fichier et exécuté le script avec les instructions :
dname = SCI+"/modules/graphics/demos/2d_3d_plots";
filename = fullfile (dname ,"contourf.dem.sce");
exec ( filename )La différence entre les deux instructions :
exec ( filename )
exec ( filename );est que la deuxième se termine par un point-virgule « ; ». Nous utilisons cet opérateur afin que Scilab n'affiche pas le contenu du dossier lorsque le script est exécuté, ce qui est pratique lorsque le script contient plusieurs lignes.
X-C. Réponses pour le chapitre III▲
Solution de l'exercice III.1 - Priorité des opérateurs
L'ordre des opérations quand ils sont appliqués à une expression mathématique est appelé la priorité. Par exemple, l'expression 2×3+4 est évaluée comme (2×3)+4. l'exemple suivant montre que la priorité des opérateurs Scilab est le même que les opérateurs mathématiques usuels.
-->2+3*4
ans =
14.
-->2/3+4
ans =
4.6666667
-->2+3/4
ans =
2.75Solution de l'exercice III.2 - Parenthèses
Lorsque la priorité des opérateurs ne calcule pas le résultat que nous voulons, les parenthèses peuvent être utilisées pour forcer l'ordre des opérations. Dans Scilab, on peut utiliser les parenthèses « ( » et « ) ».
-->2*(3+4)
ans =
14.
-->(2+3)*4
ans =
20.
-->(2+3)/4
ans =
1.25
-->3/(2+4)
ans =
0.5Solution de l'exercice III.3 - Exposants
Quand on veut définir des constantes avec des exposants, comme la constante 1.23456789×1010, nous utilisons la lettre « d » pour définir l'exposant, comme dans l'exemple suivant :
-->1.23456789d10
ans =
1.235D+10Nous pouvons également utiliser la lettre « e », comme dans l'exemple suivant qui calcule les constantes 1.23456789×1010 et 1.23456789×10-5.
-->1.23456789e10
ans =
1.235D+10
-->1.23456789e-5
ans =
0.0000123Solution de l'exercice III.4 - Fonctions
La fonction sqrt se comporte exactement comme prévu mathématiquement pour les arguments positifs.
-->sqrt(4)
ans =
2.
-->sqrt(9)
ans =
3.Pour les arguments négatifs x, Scilab retourne y comme la solution complexe de l'équation x2=y.
-->sqrt(-1)
ans =
i
-->sqrt(-2)
ans =
1.4142136iLa fonction exp est la fonction exponentielle, où la base e est le nombre d'Euler. Le log est le logarithme naturel, qui est la fonction inverse de la fonction exponentielle.
-->exp(1)
ans =
2.7182818
-->log(exp(2))
ans =
2.
-->exp(log(2))
ans =
2.La fonction log10 est le logarithme en base 10. Remarque : si x est un entier, alors log10(x) est le nombre de chiffres décimaux de x.
-->10^2
ans =
100.
-->log10(10^2)
ans =
2.
-->10^log10(2)
ans =
2.La fonction sign renvoie le signe de son argument et renvoie zéro lorsqu'il est égal à zéro.
-->sign(2)
ans =
1.
-->sign(-2)
ans =
- 1.
-->sign(0)
ans =
0.Solution de l'exercice III.5 - Trigonométrie
L'exemple suivant est un exemple d'utilisation des fonctions cos et sin.
-->cos(0)
ans =
1.
-->sin(0)
ans =
0.En raison de la précision limitée de nombres à virgule flottante, le résultat d'une fonction trigonométrique (comme toute autre fonction) est soumis à l'arrondi. Dans l'exemple suivant, l'identité mathématique sin(π)=0 est approchée au mieux, compte tenu de la précision de la machine associée aux variables doubles.
-->cos(%pi)
ans =
- 1.
-->sin(%pi)
ans =
1.225D-16
-->cos(%pi/4) - sin(%pi/4)
ans =
1.110D-16X-D. Réponses pour le chapitre IV▲
Solution de l'exercice IV.1 - Plus un
Créons le vecteur (x1+1, x2+1, x3+1, x4+1). L'exemple suivant effectue le calcul et utilise l'opérateur d'addition habituel « + ». Dans ce cas, le scalaire 1 est ajouté à chaque élément du vecteur x.
-->x = 1:4;
-->y = x+1
y =
2. 3. 4. 5.Solution de l'exercice IV.2 - Multiplication vectorisée
Supposons que x et y soient donnés. Créons le vecteur (p1, p2, p3, p4) où pi = xiyi pour i = 1, 2, 3, 4. L'exemple suivant effectue le calcul et utilise l'opérateur de multiplication élément par élément « .* ».
-->x = 1:4;
-->y = 5:8;
-->z = x.*y
z =
5. 12. 21. 32.Solution de l'exercice IV.3 - Le point infâme
Nous présentons maintenant une explication de l'exemple suivant :
-->X = 1./[2 3 4]
X =
0.0689655
0.1034483
0.1379310La cause de cela est que l'opérateur de division droite « / » calcule la solution d'une équation linéaire. La division de droite « / » est telle que X=A/B est une solution de X*B=A. Mais, dans le cas particulier où A=1 est un scalaire, la division de droite « / » est telle que X=1/B est une solution de B*X=1. En effet, dans le cas précédent, la variable 1., y compris le point, est considérée comme A.
-->B = [2 3 4]
B =
2. 3. 4.
-->X = 1/B
X =
0.0689655
0.1034483
0.1379310
-->B*X
ans =
1.Dans le cas précédent, il est plus probable que nous voulions inverser les valeurs [2 3 4]. Dans ce cas, il suffit d'insérer un espace vide entre le 1 et le point, comme dans l'exemple suivant :
-->X = 1 ./[2 3 4]
X =
0.5 0.3333333 0.25En insérant un espace vide, nous avons complètement changer le résultat. C'est parce que l'interpréteur considère maintenant la division comme une division à droite élément par élément « ./ », et divise par 1 chaque entrée de B=[2 3 4]. Cette question est parfois appelée le point infâme et cause des problèmes à la plupart des débutants.
Solution de l'exercice IV.4 - Inversion vectorisée
Créons le vecteur (1/x1, 1/x2, 1/x3, 1/x4). L'exemple suivant effectue le calcul et utilise l'opérateur de division élément par élément « ./ ».
-->x = 1:4;
-->y = 1 ./ x
y =
1. 0.5 0.3333333 0.25Solution de l'exercice IV.5 - Division vectorisée
Créons le vecteur x1/y1, x2/y2, x3/y3, x4/y4. L'exemple suivant effectue le calcul et utilise l'opérateur de division élément par élément « ./ ».
-->x = 12*(6:9);
-->y = 1:4;
-->z = x ./ y
z =
72. 42. 32. 27.Solution de l'exercice IV.6 - Carré vectorisé
Créons le vecteur x12, x22, x32, x42 avec x = 1, 2, 3, 4. L'exemple suivant effectue le calcul et utilise l'opérateur puissance élément par élément « .^ ».
-->x = 1:4;
-->y = x.^2
y =
1. 4. 9. 16.Solution de l'exercice IV.7 - Sinus vectorisé
Créons le vecteur (s1, s2, …, s10) où si = sin(xi) pour i = 1, 2, …, 10, et où les xi sont linéairement espacés dans l'intervalle [0, π]. L'exemple suivant effectue le calcul et utilise la fonction linspace.
-->x = linspace(0,%pi,10);
-->y = sin(x)
y =
column 1 to 5
0. 0.3420201 0.6427876 0.8660254 0.9848078
column 6 to 10
0.9848078 0.8660254 0.6427876 0.3420201 1.225D-16Solution de l'exercice IV.8 - Fonction vectorisée
Calculons y=f(x), les valeurs de la fonction f d'équation f(x)=log10(r/10x+10x) (1) avec r=2.220.10-16 pour x∈[-16, 0]. L'exemple suivant effectue le calcul et utilise l'opérateur de division élément par élément « ./ ».
r = 2.220D-16;
x = linspace(-16,0,10);
y = log10(r./10.^x+10.^x);Cette fonction apparaît dans le calcul du pas optimal à utiliser dans une dérivée numérique. Il montre que le pas optimal à utiliser avec une différence finie avant d'ordre un, est égale à h=sqrt(%eps).
XI. Références▲
- [1] Atlas-Automatically Tuned Linear Algebra Software. http://math-atlas.sourceforge.net ;
- [2] Cecill and free software. http://www.cecill.info ;
- [3] C Bunks, J.-P. Chancelier, F. Delebecque, C. Gomez, M. Goursat, R. Nikoukhah, and S. Steer. Engineering and Scientific Computing With Scilab. Birkhauser Boston, 1999 ;
- [4] Stephen L. Campbell, Jean-Philippe Chancelier, and Ramine Nikoukhah. Modeling and Simulation in Scilab/Scicos. Springer, 2006 ;
- [5] J.-P. Chancelier, F. Delebecque, C. Gomez, M. Goursat, R. Nikoukhah, and S. Steer. Introduction à Scilab, Deuxième Edition. Springer, 2007 ;
- [6] Intel. Intel Math Kernel Library. http://software.intel.com/en-us/intel-mkl/ ;
- [7] Sylvestre Ledru. Different execution modes of Scilab. http://wiki.scilab. org/Different_execution_modes_of_Scilab ;
- [8] Sylvestre Ledru and Yung-Jang Lee. Localization. http://wiki.scilab.org/Localization ;
- [9] Sylvestre Ledru, Pierre Mar´echal, and Simon Gareste. Atoms. http://wiki. scilab.org/ATOMS ;
- [10] Sylvestre Ledru, Pierre Maréchal, and Clément David. Code conventions for the Scilab programming language. http://wiki.scilab.org/Code%20Conventions%20for%20the%20Scilab%20Programming%20Language ;
- [11] Cleve Moler. Numerical computing with Matlab ;
- [12] Flexdock project. Flexdock project home. https://flexdock.dev.java.net/ ;
- [13] The Scilab Consortium. Scilab. http://www.scilab.org.